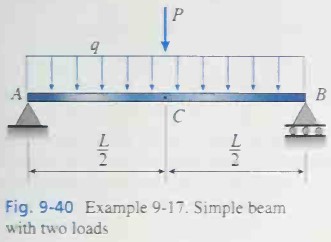
Question 9.17: A simple beam AB supports a uniform load of intensity q = 1.......
A simple beam AB supports a uniform load of intensity q = 1.5 k/ft and a concentrated load P = 5 k (Fig. 9-40). The load P acts at the midpoint C of the beam. The beam has length L = 8.0 ft. modulus of elasticity E = 30 × 10^6 psi. and moment of inertia I = 75.0 in.^4 Determine the downward deflection δ_C at the midpoint of the beam by the following methods: (1) Obtain the strain energy of the beam and use Castighano’s theorem, and (2) use the modified form of Castigliano’s theorem (differentiation under the integral sign).
Learn more on how do we answer questions.
Method (1). Because the beam and its loading are symmetrical about the midpoint, the strain energy for the entire beam is equal to twice the strain energy for the left-hand half of the beam. Therefore, we begin by finding the bending moment in the left-hand half of the beam.
The reaction at support A (Fig. 9-41) is
R_A=\frac{P}{2}+\frac{qL}{2}
and therefore the bending moment M is
M=R_Ax\ -\ \frac{qx^2}{2}=\frac{Px}{2}+\frac{qLx}{2}\ -\ \frac{qx^2}{2} (x)
in which x is measured from support A. The strain energy of the beam (from Eq. 9-80a) is
U=\int{\frac{M^2dx}{2EI}}=2\int_{0}^{L/2}{\frac{1}{2EI}\left(\frac{Px}{2}+\frac{qLx}{2}\ -\ \frac{qx^2}{2}\right)^2\ dx}
After squaring the term in parentheses and performing a lengthy integration, we find
U=\frac{P^2L^3}{96EI}+\frac{5PqL^4}{384EI}+\frac{q^2L^5}{240EI}
Since the deflection at the midpoint C (Fig. 9-40) corresponds to the load P, we can find the deflection by using Castigliano’s theorem:
δ_C=\frac{∂U}{∂P}=\frac{∂}{∂P}\left(\frac{P^2L^3}{96EI}+\frac{5PqL^4}{384EI}+\frac{q^2L^5}{240EI}\right)=\frac{PL^3}{48EI}+\frac{5qL^4}{384EI} (y)
Method (2). By using the modified form of Castigliano’s theorem (Eq. 9-88), we avoid the lengthy integration for finding the strain energy. The bending moment in the left-hand half of the beam has already been determined (see Eq. x), and its partial derivative with respect to the load P is
δ_i=\frac{∂}{∂P_i}\int{\frac{M^2dx}{2EI}=\int{\left(\frac{M}{EI}\right)\left(\frac{∂M}{∂P_i}\right)dx}} (9-88)
\frac{∂M}{∂P}=\frac{x}{2}
Therefore, the modified Castigliano’s theorem becomes
δ_C=\int{\left(\frac{M}{EI}\right)\left(\frac{∂M}{∂P}\right)dx}\\ \ \quad = 2\int_{0}^{L/2}\frac{1}{EI}\left(\frac{Px}{2}+\frac{qLx}{2}\ -\ \frac{qx^2}{2}\right)\left(\frac{x}{2}\right)dx=\frac{PL^3}{48EI}+\frac{5qL^4}{384EI} (z)
which agrees with the earlier result (Eq. y) but requires a much simpler integration.
Numerical solution. Now that we have an expression for the deflection at point C, we can substitute numerical values, as follows:
δ_C=\frac{PL^3}{48EI}+\frac{5qL^4}{384EI}\\ \ \quad =\frac{(5\ k)(96\ in.)^3}{48(30 × 10^6\ psi)(75.0\ in.^4)}+\frac{5(1.5\ k/ft)(1/12\ ft/in.)(96\ in.)^4}{384(30 × 10^6\ psi)(75.0\ in.^4)} \\ \quad = 0.0410 in. + 0.0614 in. = 0.1024 in.
Note that numerical values cannot be substituted until after the partial derivative is obtained. If numerical values are substituted prematurely, either in the expression for the bending moment or the expression for the strain energy, it may be impossible to take the derivative.
