Question 9.12: A simple beam ADB supports a concentrated load P acting at t......
A simple beam ADB supports a concentrated load P acting at the position shown in Fig. 9-26. Determine the angle of rotation θ_A at support A and the deflection δ_D under the load P. Note: The beam has a length L and constant flexural rigidity EI.


Learn more on how do we answer questions.
Use a four-step problem-solving approach.
1. Conceptualize: The deflection curve, showing the angle of rotation θ_A and the deflection δ_D, is sketched in Fig. 9-26b. The directions of θ_A and δ_D are determined by inspection, so write the moment-area expressions using only absolute values.
2. Categorize:
M/EI diagram: The bending-moment diagram is triangular, with the maximum moment (equal to Pab/L) occurring under the load. Since EI is constant, the M/EI diagram has the same shape as the moment diagram (see Fig. 9-26c).
3. Analyze:
Angle of rotation at support A: To find this angle, construct the tangent AB_1 at support A. Note that the distance BB_1 is the tangential deviation t_{B/A} of point B from the tangent at A. Calculate this distance by evaluating the first moment of the area of the M/EI diagram with respect to point B and then applying the second moment-area theorem.
The area of the entire M/EI diagram is
\quad\quad\quad\quad{\mathit{A}}_{\mathrm{i}}={\frac{1}{2}}(L){{\Bigg\lgroup}}{\frac{P a b}{L E I}}{{\Bigg\rgroup}}={\frac{P a b}{2E I}}
The centroid C_1 of this area is at distance \overline{x_1} from point B (see Fig. 9-26c). This distance, obtained from Case 3 of Appendix E, is
\quad\quad\quad\quad {\overline{{x}}}_{1}={\frac{L+b}{3}}
Therefore, the tangential deviation is
\quad\quad\quad\quad t_{B/A}=A_{1}\overline{{{x}}}_{1}=\frac{{{{P}}}a b}{2E{{{I}}}}\bigg(\frac{L+b}{3}\bigg)=\frac{{{{P}}}a b}{6E{{{I}}}}\left(L+b\right)
The angle θ_A is equal to the tangential deviation divided by the length of the beam:
\quad\quad\quad\quad\theta_{A}=\frac{t_{B/ A}}{L}=\frac{P a b}{6L E I}(L+b)\quad\quad(9-82)
Thus, the angle of rotation at support A has been found.
Deflection under the load: As shown in Fig. 9-26b, the deflection \delta_D under the load P is equal to the distance DD_1 minus the distance D_2D_1. The distance DD_1 is equal to the angle of rotation θ_A times the distance a; thus,
\quad\quad\quad\quad{{D}}{{{D}}}_{1}=a\theta_{A}={\frac{{{{P}}}a^{2}b}{6L E I}}(L+b)\quad\quad(a)
The distance D_2D_1 is the tangential deviation t_{D/A} at point D; that is, it is the deviation of point D from the tangent at A. This distance can be found from the second moment-area theorem by taking the first moment of the area of the M/EI diagram between points A and D with respect to D (see Fig. 9-26c). The area of this part of the M/EI diagram is
\quad\quad\quad\quad A_{2}={\frac{1}{2}}(a){\Bigg\lgroup}{\frac{P a b}{L E I}}{\Bigg\rgroup}={\frac{P a^{2}b}{2L E I}}
and its centroidal distance from point D is
\quad\quad\quad\quad \overline{{x}}_{2}={\frac{a}{3}}
Thus, the first moment of this area with respect to point D is
\quad\quad\quad\quad t_{D/A}=A_{2}\overline{{{x}}}_{2}={\Bigg\lgroup}\frac{P a^{2}b}{2L E I}{\Bigg\rgroup}{\Bigg\lgroup}\frac{a}{3}{\Bigg\rgroup}=\frac{P a^{3}b}{6L E I}\quad\quad(b)
The deflection at point D is
\quad\quad\delta_{D} = {D}{D}_{1}-{D}_{2}D_{1}={D}{D}_{1}-t_{D/A}
Substitute from Eqs. (a) and (b) to find
\quad\quad\quad\quad \delta_{ D}=\frac{P a^{2}b}{6L E I}(L+b)-\frac{P a^{3}b}{6L E I}=\frac{P a^{2}b^{2}}{3L E I}\quad\quad (9-83)
4. Finalize: The preceding formulas for θ_A ~ and ~ \delta_D in Eqs. (9-82) and (9-83) can be verified by using the formulas of Case 5, Table H-2, Appendix H.
| Table H-2 | |
| Deflections and Slopes of Cantilever Beams | |
 |
Notation: v = deflection in the y direction (positive upward) v’ = dv/dx = slope of the deflection curve δ_C = -v(L/2) = deflection at end B of the beam (positive downward) x_1 = distance from support A to point of maximum deflection \delta_{max} = -v_{max} = maximum deflection (positive downward) \theta_A = -v'(0) = angle of rotation at left-hand end of the beam (positive clockwise) \theta_B = v'(L) = angle of rotation at right-hand end of the beam (positive counterclockwise) EI = constant |
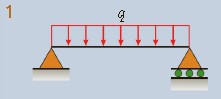 |
\begin{array}{l}{{\nu=-{\frac{q x}{24E I}}(L^{3}-2L x^{2}+x^{3})}}\\ {{\nu'=-{\frac{q}{24E I}}(L^{3}-6L x^{2}+4x^{3})}}\\ {{\mathrm{~\delta_{C}= \delta_{max}= -\frac{5qL^4}{384E I} \quad \theta_A = \theta_B = \frac{qL^3}{24EI}}}}\end{array} |
 |
\begin{array}{l}{{\nu=-{\frac{q x}{384E I}}(9L^{3} – 24L x^{2} + 16x^{3})}} \quad\quad \left(0\leq x\leq{\frac{L}{2}}\right) \\ {{\nu'=-{\frac{q}{384E I}}(9L^{3} – 72L x^{2} + 64x^{3})}}\quad\quad \left(0\leq x\leq{\frac{L}{2}}\right) \\ \nu=-{\frac{q L}{384E I}}(8x^{3} – 24L x^{2} + 17L^{2}x – L^3) \quad\quad \left(\frac{L}{2}\leq x\leq {L}\right) \\ \nu'=-{\frac{q L}{384E I}}(24x^{2} – 48L x + 17L^{2}) \quad\quad \left(\frac{L}{2}\leq x\leq {L}\right) \\ {{\mathrm{~\delta_{C}= -\frac{5qL^4}{768E I} \, \theta_A = \frac{3qL^3}{128EI} \, \theta_B = \frac{7qL^3}{384EI}}}} \end{array} |
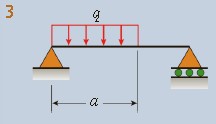 |
\begin{array}{l}{{\nu=-{\frac{q x}{24LE I}}(a^{4} – 4a^3L +4a^2L^2 + 2a^2x^2 – 4aLx^2 + Lx^{3})}} \quad\quad (0 \leq x \leq a)\\ {{\nu'=-{\frac{q}{24LE I}}(a^{4} – 4a^3L +6a^2L^2 + 6a^2x^2 – 12aLx^2 – 4Lx^{3})}} \quad\quad (0 \leq x \leq a) \\ \nu=-{\frac{q a^2}{24LE I}}(-a^{2}L + 4L^{2}x + a^2 x -6 Lx^2 + 2x^3) \quad\quad (a \leq x \leq {L})\\ \nu'=-{\frac{q A^2}{24LE I}}(4L^{2} + a^2 – 12Lx + 6x^2) \quad\quad\quad\quad (a \leq x \leq {L}) \\ {{\mathrm{~ \theta_A = \frac{qa^2}{24LEI}(2L – a)^2 \, \theta_B = \frac{qa^2}{24LEI}(2L^2 – a^2)}}} \end{array} |
 |
v=-{\frac{P x}{48E I}}(3L^{2}-4x^{2})\;\;\;\;\;v^{\prime}=-{\frac{P}{16E I}}(L^{2}-4x^{2})\;\;\;\;\left(0\leq x\leq{\frac{L}{2}}\right) \\ \delta_C = \delta_{max} = {\frac{PL^3}{48E I}}\quad\quad \theta_A = \theta_B = {\frac{PL^2}{16E I}} |
 |
\nu=-{\frac{P b x}{6L E I}}(L^{2}\,-\,b^{2}\,-\,x^{2}\,)\quad\nu^{\prime}=-{\frac{P b}{6L E I}}(L^{2}\,-\,b^{2}\,-\,3x^{2}\,)\quad(0\leq\,x\leq a) \\ \theta_A = \frac{Pab(L + a)}{6LEI} \quad \theta_B = \frac{Pab(L + a)}{6LEI} \\ If \, a ≥ b,\quad \delta_C = \frac{Pb(3L^2 – 4b^2)}{48EI} \quad If \, a \leq b,\quad \delta_C = \frac{Pa(3L^2 – 4a^2)}{48EI} \\ If \, a ≥ b,\quad x_1 = \sqrt{\frac{L^2 – b^2}{3}} \quad\quad and \quad \delta_{max}= \frac{Pb(L^2 – b^2)^{3/2}}{9\sqrt{3}LEI} |
 |
v=-{\frac{P x}{6E I}}(3aL – 3a^{2} – x^2)\;\;\;\;\;v^{\prime}=-{\frac{P}{2E I}}(aL – a^{2} – x^{2})\;\;\;\;\left(0\leq x\leq a\right) \\ v=-{\frac{P a}{6E I}}(3Lx – 3x^{2} – a^2)\;\;\;\;\;v^{\prime}=-{\frac{Pa}{2E I}}(L – 2 x)\;\;\;\;\left(a\leq x\leq L – a\right) \\ \delta_C = \delta_{max} = {\frac{Pa}{24E I}}(3L^2 – 4a^2)\quad\quad \theta_A = \theta_B = {\frac{P a (L- a)}{2E I}} |
 |
\nu=-\frac{M_{0}x}{6 LE I}(2L^{2} – 3L x + x^{2}) \quad {\nu}^{\prime}=-\frac{M_{0}}{6L E I}(2L^{2}-6L x+3x^{2}) \\ \delta_C = \frac{M_{0}L^2}{16 E I} \quad \theta_A = \frac{M_oL}{3EI} \quad \theta_B = \frac{M_o L}{6EI} \\ x_1 = L {{\Bigg\lgroup}}1 – \frac{\sqrt{3}}{3} {{\Bigg\rgroup}} \quad and \quad \delta_{max} = \frac{M_o L^2}{9\sqrt{3}EI} |
 |
\nu=-\frac{M_{0}x}{24 LE I}(L^{2} – 4x^{2}) \quad {\nu}^{\prime}=-\frac{M_{0}}{24L E I}(L^{2}-12x^{2}) \quad \left(0 \leq x \leq \frac{L}{2} \right) \\ \delta_C = 0 \quad \theta_A = \frac{M_oL}{24EI} \quad \theta_B = \frac{M_o L}{24EI} |
 |
\displaystyle{v=-\frac{M_o x}{6LE I}}(6aL – 3a^2 – 2 L^2 – x^2)\qquad(0\leq x\leq a) \\ \displaystyle{v'=-\frac{M_o }{6LE I}}(6aL – 3a^2 – 2 L^2 – 3x^2)\qquad(0\leq x\leq a) \\ At \, x= a : \displaystyle{v=-\frac{M_o ab}{3LE I}}(2a – L)\qquad \displaystyle{v'=-\frac{M_o }{3LE I}}(3aL – 3a^2 – L^2)\\ \theta_A = {\frac{M_o }{6LE I}(6 a L – 3a^2 – 2L^2)}\quad \theta_B = \frac{M_o }{6LE I}(3a^2 – L^2) |
 |
\nu=-\frac{M_{0}x}{2E I}(L – x ) \quad {\nu}^{\prime}=-\frac{M_{0}}{2 E I}(L – 2 x) \\ \delta_C = \delta_{max} = \frac{M_{0}L^2}{8 E I} \quad \theta_A = \theta_B = \frac{M_o L}{2EI} |
 |
\displaystyle{v=-\frac{q_o x}{360LE I}(7L^{4} – 10L^2 x^2 + 3Lx^{4} )} \\ \displaystyle{v'=-\frac{q_o }{360LE I}(7L^{4} – 30L^2 x^2 + 15x^{4} )} \\ \delta_C = {\frac{5q_o L^{4}}{768E I}}\quad \theta_A = \frac{7q_o L^{3}}{360E I} \quad \theta_B = \frac{q_o L^{3}}{45E I} \\ x_1 = 0.5193 L \quad \delta_{max} = 0.00652\frac{q_oL^4}{EI} |
 |
\displaystyle{v=-\frac{q_o x}{960LE I}(5L^2 – 4x^2)^2} \quad\quad \left( 0 \leq x \leq \frac{L}{2}\right) \\ \displaystyle{v'=-\frac{q_o}{192LE I}(5L^2 – 4x^2)(L^2 – 4x^2)} \quad\quad \left( 0 \leq x \leq \frac{L}{2}\right) \\ \delta_C = \delta_{max} = {\frac{q_o L^{4}}{120E I}} \quad \theta_A = \theta_B = \frac{5q_o L^{3}}{192E I} |
 |
\displaystyle{v=-\frac{q_o L^4}{\pi ^4E I}\sin {\frac{\pi x}{L}}} \quad \displaystyle{v'=-\frac{q_o L^3}{\pi ^3E I}\cos {\frac{\pi x}{L}}} \\ \delta_C = \delta_{max} = {\frac{q_o L^{4}}{\pi^4E I}} \quad \theta_A = \theta_B = \frac{q_o L^{3}}{\pi^3E I} |