Using the schema of Example E.7.1 , Fig. E.7.1, find the following: (a) Make a classification of the flows in F, P and L for each component. (b) Construct the matrices [latex]A_{F}[/latex], [latex]A_{P}[/latex] and [latex]A_{L}[/latex]. (c) Draw the installation functional diagram. (d) Construct the installation matrices [latex]a_{F}[/latex], [latex]a_{P}[/latex] and [latex]a_{L}[/latex] at its maximum level of aggregation.

Question 7.7: Using the schema of Example E.7.1, Fig. E.7.1, find the foll......

Exergy Analysis and Thermoeconomics of Buildings Design and Analysis for Sustainable Energy Systems [1399314]

Using the schema of Example E.7.1, Fig. E.7.1, find the following:
(a) Make a classification of the flows in F, P and L for each component.
(b) Construct the matrices $A_{F}$ , $A_{P}$ and $A_{L}$ .
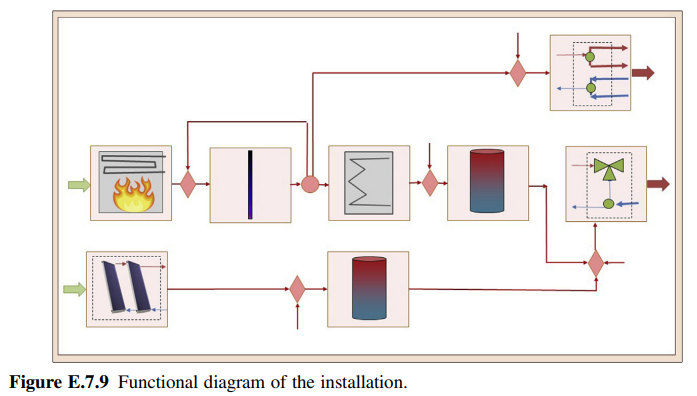
(c) Draw the installation functional diagram.
(d) Construct the installation matrices $a_{F}$ , $a_{P}$ and $a_{L}$ at its maximum level of aggregation.

Step-by-Step

The 'Blue Check Mark' means that this solution was answered by an expert.
Learn more on how do we answer questions.

(a) Table E.7.5 shows the flows classification in F, P and L for each component.

(b) The matrices $A_{F}$ , $A_{P}$ and $A_{L}$ are shown in Table E.7.6, Tables E.7.7 and E.7.8 respectively.

(c) In the functional diagram, the fuel and product are represented for each unit. For this pur-pose, virtual components are incorporated that represent the junctions and bifurcations (rhombuses and circumferences), see Fig. E.7.9. In this way, the installation productive structure is defined.

We can identify at a glance, therefore, where the fuel and the product of each component come from and where they go. This diagram also allows us to immediately locate the effect of the flows exchanged (from and to) with the outside, key information for a global study of the plant. The external inputs correspond to the fuel and solar ra-diation in the generating equipment, the storage of the tanks and the returns of the heat-ing and DHW demands.
(d) For the installation at its maximum level of aggregation, we refer again to Fig. E.7.2 and draw up the following Table E.7.9.

From Table E.7.9 we construct the matrices $a_{F}$ , $a_{P}$ and $a_{L}$ , see Table E.7.10 in which only the columns with values different to zero have been drawn.

Table E.7.5 Classification of flows in F, P and L.

	Fuel	Product	Losses
①	$\dot{B}_{21}$	${\dot{B}}_{1}\,-{\dot{B}}_{2}$	$\dot{B}_{25}$
②	$\dot{B}_{22}$	${\dot{B}}_{7}\,-{\dot{B}}_{8}$	_
③	${\dot{B}}_{1}\,-{\dot{B}}_{2}$	$(\dot{B}_{3}\,-\dot{B}_{4})\,+(\dot{B}_{5}\,-\dot{B}_{6})$	_
④	${\dot{B}}_{5}\,-{\dot{B}}_{6}$	${\dot{B}}_{9}\,-{\dot{B}}_{10}$	_
⑤	$(\dot{B}_{9}\,-\dot{B}_{10})\,+\dot{B}_{23}$	${\dot{B}}_{15}-{\dot{B}}_{16}\ -{\dot{B}}_{19}$	_
⑥	$(\dot{B}_{7}\,-\dot{B}_{8})\,+\dot{B}_{24}$	${\dot{B}}_{19}\,-{\dot{B}}_{20}$	_
⑦	${\dot{B}}_{3}\,-{\dot{B}}_{4}$	${\left[\begin{array}{l}{({\dot{B}}_{11}~-{\dot{B}}_{13})~+({\dot{B}}_{12}~-{\dot{B}}_{14})}\end{array}\right]}$	_
⑧	${\dot{B}}_{15}\,-{\dot{B}}_{16}$	${\dot{B}}_{17}\,-{\dot{B}}_{18}$	_

Table E.7.6 Matrix $A_{F}$ .

A_F =

①

②

③

-1

④

-1

⑤

-1

⑥

-1

⑦

-1

⑧

-1

Table E.7.7 Matrix $A_{P}$

A_P=

①

-1

②

-1

③

-1

④

-1

⑤

-1

⑥

-1

⑦

-1

⑧

-1

Table E.7.8 Matrix $A_{L}$

A_L=

①

②

③

④

⑤

⑥

⑦

⑧

Table E.7.9 F, P and L at the maximum level of aggregation.

	$\mathrm{Fuel}_{\mathrm{T}}$	$\mathrm{Product}_{\mathrm{T}}$	$\mathrm{Losses}_{\mathrm{T}}$
①	$\dot{B}_{21}+\dot{B}_{22}+\Delta\dot{B}_{23}+\Delta\dot{B}_{24}$	$\left({\dot{B}}_{11}\,-\,{\dot{B}}_{13}\right)\,+\,\left({\dot{B}}_{12}\,-\,{\dot{B}}_{14}\right){}{+}\left(\dot{B}_{17}\stackrel{}{-}\dot{B}_{18}\stackrel{}{-}\dot{B}_{20}\right)$	$\dot{B}_{25}$

Table E.7.10 Matrices $a_{F}$ , $a_{P}$ , $a_{L}$ at the maximum level of aggregation.

		21	22	23	24	11	12	13	14	17	18	20	25
$a_{F(1,12)}=$	T	1	1	1	1	_	_	_	_	_	_	_	_
		21	22	23	24	11	12	13	14	17	18	20	25
$a_{P(1,12)}=$	T	_	_	_	_	1	1	-1	-1	1	-1	-1	_
		21	22	23	24	11	12	13	14	17	18	20	25
$a_{L(1,12)}=$	T	_	_	_	_	_	_	_	_	_	_	_	1