Question 11.2: A stream consisting of 5000 lb/h of saturated n-propyl alcoh...

(a) The physical properties given in Example 11.1 will be used as a first approximation. Values of k_{L}  \text{and}  \rho_{L} will be assumed constant, but the variation of \mu_{L} with temperature will be accounted for. As in Example 11.1, the density of the vapor will be neglected compared with that of the liquid. The first step is to compute the Reynolds number:

\Gamma=\frac{W}{n_{ t } \pi D_{i}}=\frac{5000}{109 \pi(0.584 / 12)}=300.0  lbm / ft \cdot h

R e=\frac{4 \Gamma}{\mu_{L}}=\frac{4  \times  300.0}{0.5  \times  2.419}=992.1

The flow regime is wavy laminar, so Equation (11.44) is used to calculate the heat-transfer coefficient:

h=\frac{\operatorname{Re}\left[k_{L}^{3} \rho_{L} (\rho_{L}  –  \rho_{V}) g / \mu_{L}^{2}\right]^{1 / 3}}{1.08 R e^{1.22}  –  5.2}               (11.44)

h=\frac{\operatorname{Re}\left[k_{L}^{3} \rho_{L}^{2} g / \mu_{L}^{2}\right]^{1 / 3}}{1.08 R e^{1.22}  –  5.2}

=\frac{992.1\left[(0.095)^{3}(49)^{2}\left(4.17 \times 10^{8}\right) /(0.5 \times 2.419)^{2}\right]^{1 / 3}}{1.08(992.1)^{1.22}  –  5.2}

    h = 170 Btu/h·ft²·ºF

Next, the temperature drop across the condensate film is calculated. From Table A.17, the latent heat of vaporization is:

\lambda=164.36  cal / g  \times  1.8 \frac{ Btu / lbm }{ cal / g }=295.85  Btu / lbm

Neglecting the sensible heat of subcooling, the duty is:

q = Wλ = 5000 × 295.85 = 1,479, 250 Btu/h

q=hn _{ t } \pi D_{ i } L \Delta T

\Delta T=\frac{q}{h n_{t} \pi D_{i} L}=\frac{1,479,250}{170 \times 109 \pi(0.584 / 12) \times 12}=43.5^{\circ} F

Therefore, the wall temperature is:

T_{w} = 207-43.5=163.5^{\circ} F

The weighted average film temperature is calculated from Equation (11.43):

T_{f}=0.75  T_{w}+0.25  T_{\text {sat }}=0.75  \times  163.5+0.25  \times  207

T_{f}=174.4^{\circ} F

From Figure A.1, the condensate viscosity at this temperature is 0.7 cp. A second iteration is made using this value of \mu_{L} :

R e=\frac{4  \times  300.0}{0.7  \times  2.419}=708.7 \Rightarrow \text { wavy laminar flow }

h=\frac{708.7\left[(0.095)^{3}(49)^{2}\left(4.17  \times  10^{8}\right) /(0.7  \times  2.419)^{2}\right]^{1 / 3}}{1.08(708.7)^{1.22}  –  5.2} \cong 146  Btu / h \cdot ft ^{2} \cdot{ }^{\circ} F

\Delta T=\frac{1,479,250}{146  \times  109 \pi(0.584 / 12)  \times  12}=50.7^{\circ} F

T_{w}=207-50.7=156.3^{\circ} F

T_{f}=0.75 \times 156.3+0.25 \times 207 \cong 169^{\circ} F

At this value of T_{f}, the condensate viscosity is 0.73 cp. Results of the third iteration are given below:

      Re = 679.6

h ≅ 144 Btu/h·ft²·ºF

ΔT = 51.4º F

        T_{w} = 155.6º F

T_{f} = 168.5º F

Since the new value of T_{f} is close to the previous value, no further iterations are required.
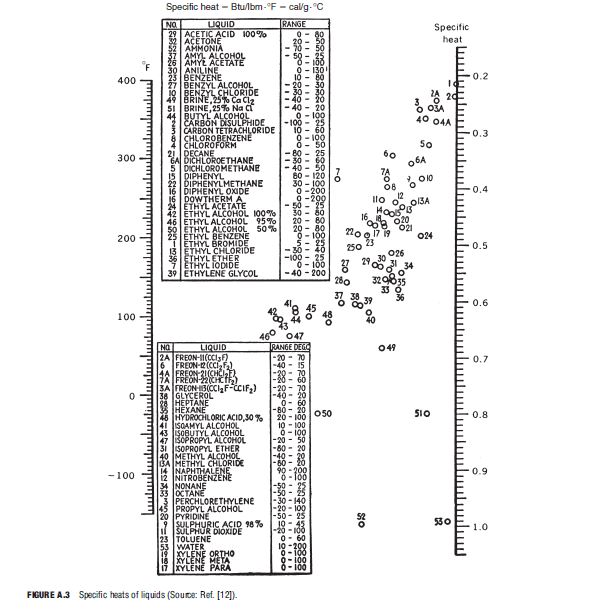
To check the effect of subcooling on h, the condensate Prandtl number is computed next. The heat capacity of liquid n-propyl alcohol at T_{f} ≅ 169º F is found from Figure A.3: C_{P,L} = 0.72 Btu/lbm·ºF. Thus,

\epsilon=\frac{C_{P, L}\left(T_{s a t}  –  T_{w}\right)}{\lambda}=\frac{0.72(207  –  155.6)}{295.85}=0.125

Using Equation (11.52) we obtain:

h / h_{N u}=\left[1+\left(0.683-0.228 Pr_{L}^{-1}\right) \epsilon\right]^{1 / 4}

=[1+(0.683-0.228 / 13.4)  \times  0.125]^{1 / 4}

h / h_{N u}=1.020

For comparison, the calculation is also done using Equation (11.53):

h / h_{ Nu }=\left(\frac{1  +  0.68  \epsilon  +  0.02  \epsilon^{2} Pr_{L}^{-1}}{1  +  0.85  \epsilon  Pr_{L}^{-1}  –  0.15  \epsilon^{2} Pr_{L}^{-1}}\right)^{1 / 4}

=\left\{\frac{1  +  0.68  \times  0.125  +  0.02(0.125)^{2} / 13.4}{1  +  0.85  \times  0.125 / 13.4  –  0.15(0.125)^{2} / 13.4}\right\}^{1 / 4}

h / h_{ Nu }=1.019

Thus, both methods predict an increase in h of about 2% due to condensate subcooling. Including this effect gives h ≅ 147 Btu/ h · ft²·º F. This correction is not large enough to warrant further iteration.
(b) The physical properties from Example 11.1 are again used to initialize the calculations and the vapor density is neglected. The heat-transfer coefficient is computed using Equations (11.40) and (11.41):

h=1.52\left[\frac{k_{L}^{3} \rho_{L}(\rho_{L}  –  \rho_{V}) g}{4 \mu_{L} \Gamma^{*}}\right]^{1 / 3}                  (11.40)

\Gamma^{*}=\frac{W}{L n_{ t }^{2 / 3}}=\frac{5000}{12(109)^{2 / 3}}=18.26  lbm / ft \cdot h

h=1.52\left[\frac{k_{L}^{3} \rho_{L}^{2} g}{4 \mu_{L} \Gamma^{*}}\right]^{1 / 3}=1.52\left[\frac{(0.095)^{3}(49)^{2}\left(4.17 \times 10^{8}\right)}{4(0.5 \times 2.419) \times 18.26}\right]^{1 / 3}

h = 324 Btu/h·ft²·ºF

Next, the temperature difference across the condensate film is calculated:

\Delta T=T_{\text {sat }}-T_{w}=\frac{q}{h n_{ t } \pi D_{0} L}=\frac{1,479,250}{324  \times  109 \pi(0.75 / 12)  \times  12}

ΔT = 17.8º F

T_{w} = 207 – 17.8 = 189.2º F

T_{f}=0.75  T_{w}+0.25  T_{\text {sat }}=0.75  \times  189.2  +  0.25  \times  207=193.7^{\circ} F

From Figure A.1, the condensate viscosity at T_{f} is 0.58 cp. The above calculations are repeated using this value of viscosity.

h=1.52\left[\frac{(0.095)^{3}(49)^{2}\left(4.17 \times 10^{8}\right)}{4(0.58 \times 2.419) \times 18.26}\right]^{1 / 3} \cong 309  Btu / h \cdot ft ^{2} \cdot{ }^{\circ} F

\Delta T=\frac{1,479,250}{309  \times  109 \pi(0.75 / 12)  \times  12}=18.6^{\circ} F

T_{w}=207-18.6=188.4^{\circ} F

T_{f}=0.75  \times  188.4  +  0.25  \times  207=193^{\circ} F

Since the new value of T_{f} is close to the previous value, the calculations have converged.
Using Equation (11.52) to estimate the effect of condensate subcooling for this case yields h / h_{ Nu } = 1.0076. Including this minor correction gives h = 311 Btu/h . ft².º F. Clearly, the effect of  condensate subcooling is negligible in this case.