Question 18.2: An amplifier with an input capacitance of Cin is to be ac-co...
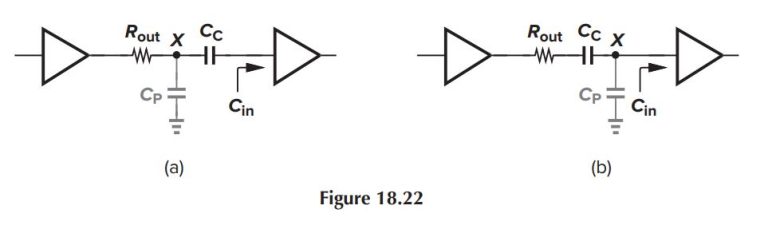
An amplifier with an input capacitance of C_{i n} is to be ac-coupled to a preceding stage having an output resistance R_{\text {out }}. Considering both of the topologies depicted in Fig. 18.22 and allowing a maximum signal attenuation of 20 \%, determine the minimum value of the coupling capacitor and the resulting time constant if C_P=0.5 C_C or C_P=0.2 C_C.
In Fig. 18.22(a), the attenuation is given by A_v=C_C /\left(C_C+C_{i n}\right), yielding C_C \geq 4 C_{i n} for a 20% signal loss. The total capacitance seen from node X to ground is therefore equal to C_P+C_C C_{i n} /\left(C_C+C_{i n}\right)=C_P+0.8 C_{i n}. It follows that the time constant is 2.8 R_{\text {out }} C_{\text {in }} for C_P=0.5 C_C and 1.6 R_{\text {out }} C_{\text {in }} for C_P=0.2 C_C.
In Fig. 18.22(b), C_P itself attenuates the signal: A_v=C_C /\left(C_C+C_{i n}+C_P\right), indicating that no value of C_C can yield a signal loss of 20% if C_P \geq 0.25 C_C.
These calculations yield two important results. First, the topology of Fig. 18.22(a) is generally preferable. Second, the addition of a coupling capacitor, e.g., to isolate the bias levels, substantially degrades the speed.