Question 7.7: An element of material in plane strain undergoes the followi...
An element of material in plane strain undergoes the following strains:
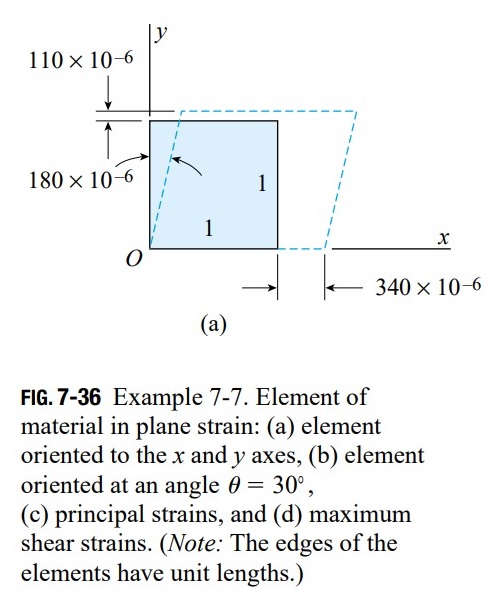
\epsilon_{x}=340\times10^{-6} \epsilon_{y}=110\times10^{-6} \gamma_{xy}=180\times10^{-6}
These strains are shown highly exaggerated in Fig. 7-36a, which shows the deformations of an element of unit dimensions. Since the edges of the element have unit lengths, the changes in linear dimensions have the same magnitudes as the normal strains \epsilon_{x} and \epsilon_{y}. The shear strain \gamma_{xy} is the decrease in angle at the lower-left corner of the element.
Determine the following quantities: (a) the strains for an element oriented at an angle θ = 30° , (b) the principal strains, and (c) the maximum shear strains. (Consider only the in-plane strains, and show all results on sketches of properly oriented elements.)
Learn more on how we answer questions.
(a) Element oriented at an angle θ = 30° . The strains for an element oriented at an angle θ to the x axis can be found from the transformation equations (Eqs. 7-71a and 7-71b). As a preliminary matter, we make the following calculations:
\frac{\epsilon_{x}+\epsilon_{y}}{2}=\frac{(340+110)10^{-6}}{}=225\times10^{-6}
\frac{\epsilon_{x}-\epsilon_{y}}{2}=\frac{(340-110)10^{-6}}{}=115\times10^{-6}
\frac{\gamma_{xy}}{2}=90\times10^{-6}
Now substituting into Eqs. (7-71a) and (7-71b), we get
\epsilon_{x_{1}}=\frac{\epsilon_{x}+\epsilon_{y}}{2}+\frac{\epsilon_{x}-\epsilon_{y}}{2}\cos2\theta+\frac{\gamma_{xy}}{2}\sin2\theta (7-71a)
=(225\times10^{-6})+(115\times10^{-6})(\cos60^{\circ})+(90\times10^{-6})(\sin60^{\circ})
=360\times10^{-6}
\frac{\gamma_{x_{1}y_{1}}}{2}=-\frac{\epsilon_{x}-\epsilon_{y}}{2}\sin2\theta+\frac{\gamma_{xy}}{2}\cos2\theta (7-71b)
=-(115\times10^{-6})(\sin 60^{\circ})+(90\times10^{-6})(\cos60^{\circ})
=-55\times10^{-6}
Therefore, the shear strain is
\gamma_{x_{1}y_{1}}=-110\times10^{-6}The strain \epsilon_{y_{1}} can be obtained from Eq. (7-72), as follows:
\epsilon_{x_{1}}+\epsilon_{y_{1}}=\epsilon_{x}+\epsilon_{y} (7-72)
\epsilon_{y_{1}}=\epsilon_{x}+\epsilon_{y}-\epsilon_{x_{1}}=(340+110-360)10^{-6}=90\times10^{-6}The strains \epsilon_{x_{1}}, \epsilon_{y_{1}}, and \gamma_{x_{1}y_{1}} are shown in Fig. 7-36b for an element oriented at θ = 30° . Note that the angle at the lower-left corner of the element increases because \gamma_{x_{1}y_{1}} is negative.
(b) Principal strains. The principal strains are readily determined from Eq. (7-74), as follows:
=225\times10^{-6}\pm\sqrt{\left(115\times10^{-6}\right)^{2}+\left(90\times10^{-6}\right)^{2}}
=225\times10^{-6}\pm146\times10^{-6}
Thus, the principal strains are
\epsilon_{1}=370\times10^{-6} \epsilon_{2}=80\times10^{-6}
in which \epsilon_{1} denotes the algebraically larger principal strain and \epsilon_{2} denotes the algebraically smaller principal strain. (Recall that we are considering only in-plane strains in this example.)
The angles to the principal directions can be obtained from Eq. (7-73):
The values of 2\theta_{p} between 0 and 360° are 38.0° and 218.0° , and therefore the angles to the principal directions are
\theta_{p} = 19.0° and 109.0°
To determine the value of \theta_{p} associated with each principal strain, we substitute \theta_{p} = 19.0° into the first transformation equation (Eq. 7-71a) and solve for the strain:
\epsilon_{x_{1}}=\frac{\epsilon_{x}+\epsilon_{y}}{2}+\frac{\epsilon_{x}+\epsilon_{y}}{2}\cos2\theta+\frac{\gamma_{xy}}{2}\sin2\theta=(225\times10^{-6})+(115\times10^{-6})(\cos38.0^{\circ})+(90\times10^{-6})(\sin38.0^{\circ})
=370\times10^{-6}
This result shows that the larger principal strain \epsilon_{1} is at the angle \theta_{p_{1}} = 19.0° . The smaller strain \epsilon_{2} acts at 90° from that direction (\theta_{p_{2}} = 109.0°). Thus,
\epsilon_{1}=370\times10^{-6} and \theta_{p_{1}} = 19.0°
\epsilon_{2}=80\times10^{-6} and \theta_{p_{2}} = 109.0°
Note that \epsilon_{1} + \epsilon_{2} = \epsilon_{x} + \epsilon_{y}.
The principal strains are portrayed in Fig. 7-36c. There are, of course, no shear strains on the principal planes.
(c) Maximum shear strain. The maximum shear strain is calculated from Eq. (7-75):
The element having the maximum shear strains is oriented at 45° to the principal directions; therefore, \theta_{s} = 19.0° + 45° = 64.0° and 2\theta_{s} = 128.0° . By substituting this value of 2\theta_{s} into the second transformation equation (Eq. 7-71b), we can determine the sign of the shear strain associated with this direction. The calculations are as follows:
\frac{\gamma_{x_{1}y_{1}}}{2}=-\frac{\epsilon_{x}-\epsilon_{y}}{2}\sin2\theta+\frac{\gamma_{xy}}{2}\cos2\theta=-(115\times10^{-6})(\sin 128.0^{\circ})+(90\times10^{-6})(\cos 128.0^{\circ})
=-146\times10^{-6}
This result shows that an element oriented at an angle \theta_{s_{2}} = 64.0° has the maximum negative shear strain.
We can arrive at the same result by observing that the angle \theta_{s_{1}} to the direction of maximum positive shear strain is always 45° less than \theta_{p_{1}}. Hence,
\theta_{s_{1}}=\theta_{p_{1}}-45^{\circ}=19.0^{\circ}-45^{\circ}=-26.0^{\circ}
\theta_{s_{2}}=\theta_{s_{1}}+90^{\circ}=64.0^{\circ}
The shear strains corresponding to \theta_{s_{1}} and \theta_{s_{2}} are \gamma_{\max} = 290 × 10^{-6} and \gamma_{\min} = -290 × 10^{-6}, respectively.
The normal strains on the element having the maximum and minimum shear strains are
A sketch of the element having the maximum in-plane shear strains is shown in Fig. 7-36d.
In this example, we solved for the strains by using the transformation equations. However, all of the results can be obtained just as easily from Mohr’s circle.
