Question 17.2: Computing Earliest Starting and Finishing Times Compute the ...
Computing Earliest Starting and Finishing Times
Compute the earliest starting time and earliest finishing time for each activity in the diagram shown in Figure 17.5.
Begin by placing brackets at the two ends of each starting activity:
We want to determine and place in the brackets for each activity the earliest starting time, ES, and the earliest finishing time, EF, for every activity, and put them in brackets, as follows:
Do this for all activities, beginning at the left side of the precedence diagram and moving to the right side.
Once ES has been determined for each activity, EF can be found by adding the activity time, t, to ES: ES + t = EF.
Use an ES of 0 for all starting activities. Thus, activities 1-2 and 1-3 are assigned ES values of 0. This permits computation of the EF for each of these activities:
EF1-2 = 0 + 8 = 8 and EF1-3 = 0 + 4 = 4
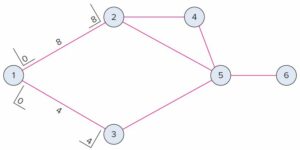
The EF time for an activity becomes the ES time for the next activity to follow it in the diagram. Hence, because activity 1-2 has an EF time of 8, both activities 2-4 and 2-5 have ES times of 8. Similarly, activity 3-5 has an ES time of 4.
This permits calculation of the EF times for these activities: EF2-4 = 8 + 6 = 14; EF2-5 = 8 + 11 = 19; and EF3-5 = 4 + 9 = 13.
The ES for activity 4-5 is the EF time of activity 2-4, which is 14. Using this value, we find the EF for activity 4-5 is 17; EF4-5 = 14 + 3 = 17.
In order to determine the ES for activity 5-6, we must realize that activity 5-6 cannot start until every activity that precedes it is finished. Therefore, the largest of the EF times for the three activities that precede activity 5-6 determines ES5-6. Hence, the ES for activity 5-6 is 19.
Then the EF for the last activity, 5-6, is 20; EF5-6 = 19 + 1 = 20. Note that the latest EF is the project duration. Thus, the expected length of the project is 20 weeks.