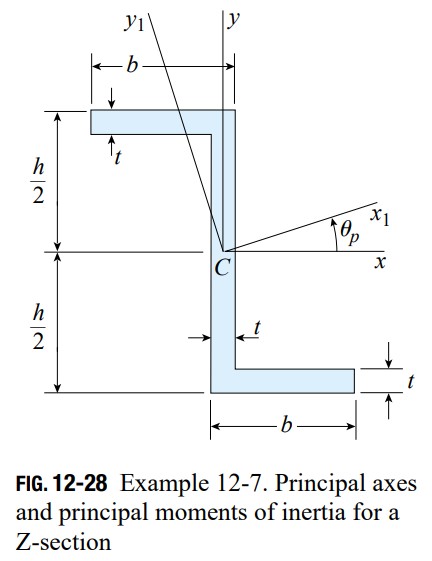
Question 12.7: Determine the orientations of the principal centroidal axes ...

Let us use the xy axes (Fig. 12-28) as the reference axes through the centroid C. The moments and product of inertia with respect to these axes can be obtained by dividing the area into three rectangles and using the parallel-axis theorems. The results of such calculations are as follows:

$I_{x}=29.29\times10^{6}  mm^{4}$        $I_{y}=5.667\times10^{6}  mm^{4}$        $I_{xy}=-9.366\times10^{6}  mm^{4}$

Substituting these values into the equation for the angle $\theta_{p}$ (Eq. 12-30), we get

$\tan2\theta_{p}=-\frac{2I_{xy}}{I_{x}-I_{y}}=0.7930$      $2\theta_{p}$ = 38.4° and 218.4°

Thus, the two values of $\theta_{p}$ are

$\theta_{p}$ = 19.2° and 109.2°

Using these values of $\theta_{p}$ in the transformation equation for $I_{x_{1}}$ (Eq. 12-25), we find $I_{x_{1}} = 32.6 × 10^{6}  mm^{4}$ and $2.4 × 10^{6}  mm^{4}$, respectively. These same values are obtained if we substitute into Eqs. (12-33a) and (12-33b). Thus, the principal moments of inertia and the angles to the corresponding principal axes are

$I_{x_{1}}=\frac{I_{x}+I_{y}}{2}+\frac{I_{x}-I_{y}}{2}\cos2\theta-I_{xy}\sin2\theta$                    (12-25)

$I_{1}=\frac{I_{x}+I_{y}}{2}+\sqrt{\left(\frac{I_{x}-I_{y}}{2}\right)^{2}+I^{2}_{xy}}$              (12-33a)

$I_{2}=\frac{I_{x}+I_{y}}{2}-\sqrt{\left(\frac{I_{x}-I_{y}}{2}\right)^{2}+I^{2}_{xy}}$              (12-33b)

$I_{1} = 32.6 × 10^{6}  mm^{4}$        $\theta_{p_{1}}$ = 19.2°

$I_{2} = 2.4 × 10^{6}  mm^{4}$        $\theta_{p_{2}}$ = 109.2°

The principal axes are shown in Fig. 12-28 as the $x_{1}y_{1}$ axes.