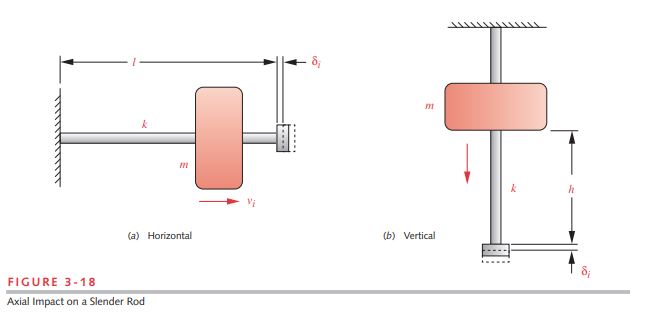
Impact Loading on an Axial Rod Problem: The axial rod shown in Figure 3-18a is hit by a mass moving at 1 m/sec. a. Determine the sensitivity of the impact force to the length/diameter ratio of the rod for a constant 1-kg moving mass. b. Determine the sensitivity of the impact force to the ratio of

Question

Impact Loading on an Axial Rod

Problem: The axial rod shown in Figure [latex]3-18a[/latex] is hit by a mass moving at 1 m/sec.

a. Determine the sensitivity of the impact force to the length/diameter ratio of the rod for a constant 1-kg moving mass.

b. Determine the sensitivity of the impact force to the ratio of moving mass to rod mass for a constant length/diameter ratio of 10.

Given: The round rod is 100 mm long. The rod and moving mass are steel with [latex]E[/latex] = 207 Gpa and a mass density of 7.86 g/cm³.

Assumptions: An approximate energy method will be acceptable. The correction factor for energy dissipation will be applied.

Accepted Answer

See Figures 3-18a, 3-20, and 3-21.

1 Figure [latex]3-18a[/latex] shows the system. The moving mass strikes the flange on the end of the rod with the stated velocity of 1 m/sec.

2 For part ([latex]a[/latex]), we will keep the moving mass constant at 1 kg, and the rod length constant at 100 mm and vary the rod diameter to obtain [altex]l/d[/latex] ratios in the range of 1 to 20. In the equations that follow we will show only one calculation made for the [latex]l/d[/latex] ratio of 10. We can also compute all the values for a list of [latex]l/d[/latex] ratios. The static deflection that would result from application of the weight force of the mass is calculated from the expression for the deflection of a bar in tension. (See equation 4.8 in the next chapter for the derivation.)

[latex] \Delta s=\frac{P l}{A E} [/latex] (4.8)

[latex] \delta_{s t}=\frac{W l}{A E}=\frac{9.81 N (100 mm )}{78.54 mm ^2\left(2.07 E 5 N / mm ^2 ight)}=0.06 \mu m [/latex] (a)

The correction factor η is calculated here for an assumed mass ratio of 16.2,

[latex] \eta=\frac{1}{1+\frac{m_b}{3 m}}=\frac{1}{1+\frac{0.0617}{3(1)}}=0.98 [/latex] (b)

These values (calculated for each different rod diameter [latex]d[/latex]) are then substituted into equation 3.12 to find the force ratio [latex]F_{i} / W[/latex] and the dynamic force [latex]F_{i }[/latex]. For [latex]d[/latex] = 10 mm

[latex] \frac{F_i}{W}=\frac{\delta_i}{\delta_{s t}}=v_i \sqrt{\frac{\eta}{g \delta_{s t}}} [/latex] (3.12)

[latex] \begin{array}{l} \frac{F_i}{W}=v_i \sqrt{\frac{\eta}{g \delta_{s t}}}=1 \frac{ m }{ s } \sqrt{\frac{0.98}{9.81 \frac{ m }{ s ^2}(0.00006 m )}}=1285.9 \ F_i=1285.9(9.81 N )=12612 N \end{array} [/latex] (c)

The variation in force ratio with changes in [latex]l/d[/latex] ratio for a constant amount of moving mass and a constant impact velocity (i.e., constant input energy) is shown in Figure 3-20. As the [latex]l/d[/latex] ratio is reduced, the rod becomes much stiffer and generates much larger dynamic forces from the same impact energy. This clearly shows that impact forces can be reduced by increasing the compliance of the impacted system.

3 For part ([latex]b[/latex]), we will keep the [latex]l/d[/latex] ratio constant at 10 and vary the ratio between the moving mass and the rod mass over the range of 1 to 20. The files EX03-01B on the CD-ROM calculate all values for a range of mass ratios. The results for a mass ratio of 16.2 are the same as in part ([latex]a[/latex]) above. Figure [latex]3-21a[/latex] shows that the dynamic force ratio [latex]F_{i} / W[/latex] varies inversely with the mass ratio. However, the value of the dynamic force is increasing with mass ratio as shown in Figure 3-21b, because the static force [latex]W[/latex] is also increasing with mass ratio.

Question 3.1: Impact Loading on an Axial Rod Problem: The axial rod shown ...

Related Answered Questions

Fourbar Linkage Loading Analysis Problem: Determine the theoretical rigid-body forces acting in two dimensions on the fourbar linkage shown in Figure 3-11. Given: The linkage geometry, masses, and mass moments of inertia are known and the linkage is driven at up to 120 rpm by a speed-controlled ...

Verified Answer:

Verified Answer:

Verified Answer:

Shear and Moment Diagrams of a Cantilever Beam Using Singularity Functions Problem: Determine and plot the shear and moment functions for the cantilever beam with a concentrated load as shown in Figure 3-22b. Given: Beam length l = 10 in, and load location a = 4 in. The magnitude of the applied ...

Verified Answer:

Verified Answer:

Shear and Moment Diagrams of an Overhung Beam Using Singularity Functions Problem: Determine and plot the shear and moment functions for the overhung beam with an applied moment and ramp load as shown in Figure 3-22c. Given: Beam length l = 10 in, and load location a = 4 in. The magnitude of the ...

Verified Answer:

Verified Answer:

Shear and Moment Diagrams of a Simply Supported Beam Using a Graphical Method Problem: Determine and plot the shear and moment functions for the simply supported beam with uniformly distributed load shown in Figure 3-22a. Given: Beam length l = 10 in, and load location a = 4 in. The magnitude of ...

Verified Answer:

Automobile Scissors-Jack Loading Analysis Problem: Determine the forces on the elements of the scissors jack in the position shown in Figure 3-5. Given: The geometry is known and the jack supports a force of P = 1 000 lb (4 448 N) in the position shown. Assumptions: The accelerations are ...

Verified Answer:

Hand-Operated Crimping-Tool Loading Analysis Problem: Determine the forces on the elements of the crimping tool shown in Figure 3-3 during a crimp operation. Given: The geometry is known and the tool develops a crimp force of 2 000 lb (8 896 N) at closure in the position shown. Assumptions: The ...

Verified Answer: