Question 2.24: In N = {e1^→, e2^→}, let f: R2 → R2 be defined as f(x1, x2) ...
In N=\left\{\overrightarrow{e_{1} }, \overrightarrow{e_{2} }\right\}, let f: R² → R² be defined as
f\left(x_{1},x_{2} \right) =\left(x_{1}+\frac{1}{2}x_{2}, -\frac{1}{2}x_{1}+2x_{2} \right)
=\overrightarrow{x}A, where \overrightarrow{x}=\left(x_{1},x_{2} \right) and A=\begin{bmatrix} 1 & -\frac{1}{2} \\ \frac{1}{2} & 2 \end{bmatrix}.
Investigate mapping properties of A.
Learn more on how we answer questions.
f is isomorphic. Its characteristic polynomial is
det\left(A-tI_{2} \right)=\left|\begin{matrix} 1-t & -\frac{1}{2} \\ \frac{1}{2} & 2-t \end{matrix} \right| =\left(t-\frac{3}{2} \right) ^{2} .
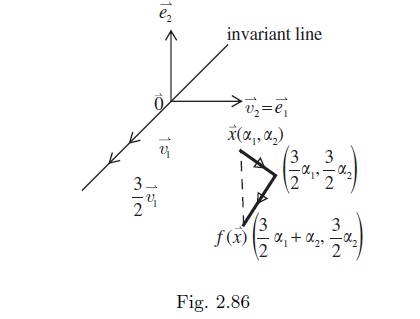
Therefore, f or A has eigenvalues \frac{3}{2},\frac{3}{2} and A is not diagonalizable. Solve \overrightarrow{x}\left(A-\frac{3}{2}I_{2} \right)=0 and we get the corresponding eigenvectors t\left(1,1 \right) for t≠ 0. Hence, it is expected that x_{1}-x_{2}=0 is an invariant line (subspace) of A.
Of course, A satisfies its characteristic polynomial, i.e.
A^{2}-3A+\frac{9}{4}I_{2} =\left(A-\frac{3}{2}I_{2}\right) ^{2}=O.
Thus
G=\left\{\overrightarrow{x }\in R^{2}\mid \overrightarrow{x } \left(A-\frac{3}{2}I_{2}\right) ^{2}=\overrightarrow{0 }\right\} =R^{2}.
Take a vector, say \overrightarrow{e_{1} }=\left(1,0\right), so that
\overrightarrow{e_{1} }\left(A-\frac{3}{2}I_{2}\right)= \left(-\frac{1}{2},-\frac{1}{2}\right)=-\frac{1}{2}\left(\overrightarrow{e_{1} }+\overrightarrow{e_{2} }\right)\neq \overrightarrow{0},
\overrightarrow{e_{1} }\left(A-\frac{3}{2}I_{2}\right) ^{2}=\overrightarrow{0 }.
Then B= \left\{\overrightarrow{v_{1} },\overrightarrow{v_{2} }\right\}, where \overrightarrow{v_{1} }=-\frac{1}{2}\left(\overrightarrow{e_{1} }+\overrightarrow{e_{2} }\right) and \overrightarrow{v_{2} }=\overrightarrow{e_{1} }, is a basis for R². Related to B,
\overrightarrow{v_{1} }A=\frac{3}{2}\overrightarrow{v_{1} }=\frac{3}{2}\overrightarrow{v_{1} }+0\cdot \overrightarrow{v_{2} },
\overrightarrow{v_{2} }A=\frac{3}{2}\overrightarrow{e_{1} }-\frac{1}{2}\left(\overrightarrow{e_{1} }+\overrightarrow{e_{2} }\right)=\overrightarrow{v_{1} } +\frac{3}{2}\overrightarrow{v_{2} }
\Rightarrow \left[F\right] _{B}=PAP^{-1}= \begin{bmatrix} \frac{3}{2} & 0 \\ 1 & \frac{3}{2} \end{bmatrix} = \frac{3}{2}I_{2}+\begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix} ,
where
P=\left[\begin{matrix} \overrightarrow{v_{1} } \\ \overrightarrow{v_{2} } \end{matrix} \right] =\begin{bmatrix} -\frac{1}{2} & -\frac{1}{2} \\ 1 & 0 \end{bmatrix}.
For any \overrightarrow{x }\in R^{2},
\overrightarrow{x}=\left(x_{1},x_{2} \right) in N=\left\{\overrightarrow{e_{1} }, \overrightarrow{e_{2} }\right\} \\\ \downarrow \\\ \left[\overrightarrow{x} \right] _{B}=\left(\alpha _{1},\alpha _{2} \right) in B= \left\{\overrightarrow{v_{1} }, \overrightarrow{v_{2} }\right\} \\\ \downarrow \\\ \left[f\left(\overrightarrow{x}\right) \right] _{B}= \left[\overrightarrow{x} \right] _{B}\left[f \right] _{B}= \frac{3}{2}\left(\alpha _{1},\alpha _{2} \right)+\left(\alpha _{2}, 0\right) \\\ \quad \quad \quad\quad \quad\quad \quad \quad \quad \quad = \left(\frac{3}{2}\alpha _{1}+\alpha _{2} ,\frac{3}{2}\alpha _{2} \right) in B \\\ \downarrow \\\ f\left(\overrightarrow{x} \right)= \overrightarrow{x}A=\overrightarrow{x}P^{-1} \left[f \right] _{B} P= \left(x_{1}+\frac{1}{2}x_{2},-\frac{1}{2}x_{1}+2x_{2} \right)\in R^{2} in NThis means that \ll \overrightarrow{v_{1} } \gg, i.e. x_{1}-x_{2}=0, is the only invariant line (subspace) of f, on which each point \overrightarrow{x} is moved to f \left( \overrightarrow{x}\right) =\frac{3}{2}\overrightarrow{x}. See Fig. 2.86.