Question 8.2: LOW-PASS COMPOSITE FILTER DESIGN Design a low-pass composite...

All of the component values can be found from Table 8.2

Low-Pass	High-Pass
Constant-k T section	Constant-k T section
\ R_{0}=\sqrt{L/C}     L=2R_{0}/\omega _{c}	\ R_{0}=\sqrt{L/C}     L=R_{0}/2\omega _{c}
\ \omega _{c}=2/\sqrt{LC}     C=2/\omega _{c}R_{0}	\ \omega _{c}=1/2\sqrt{LC}     C=1/2\omega _{c}R_{0}
m-derived T section	m-derived T section
L, C Same as constant-k section	L, C Same as constant-k section
\ m=\sqrt{1-\left(\omega _{c}/\omega _{\infty }\right)^{2} }	\ m=\sqrt{1-\left(\omega _{c}/\omega _{\infty }\right)^{2} }
Bisected- matching section	Bisected- matching section

. For the constant-k section

For the m = 0.6 matching sections

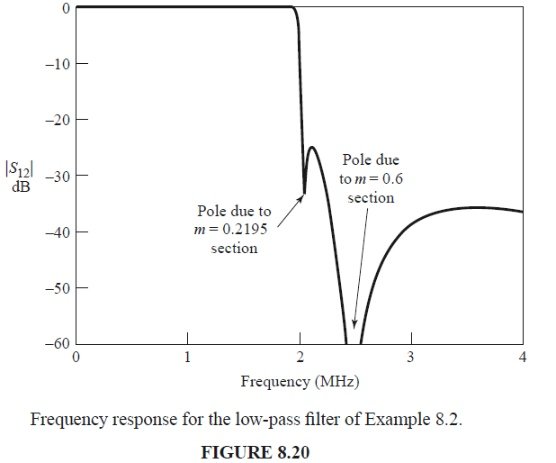
The completed filter circuit is shown in Figure 8.19; the series pairs of inductors between the sections have been combined. Figure 8.20 shows the resulting frequency response for |S12|. Note the sharp dip at f = 2.05 MHz due to the m = 0.2195 section, and the pole at 2.50 MHz, which is due to the m = 0.6 matching sections.