Question 10.6: Refer to Example 10.4. If the san1ple size remains at n = 4,...
Refer to Example 10.4. If the san1ple size remains at n = 4, what must the value of the process standard deviation a be to produce an ARL of 10 when the process mean shifts to 3.5?
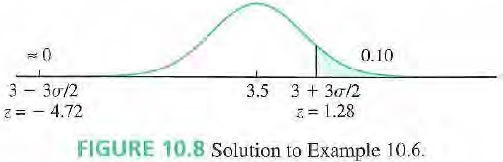
Let σ denote the new process standard deviation. The new control limits are 3 \pm 3 \sigma / \sqrt{n}, or 3 \pm 3 \sigma / 2. If the process mean shifts to 3.5, then \bar{X}\sim N\left(3.5, \sigma^2 / 4\right). The probability that \bar{X} plots outside the control limits is equal to P(\bar{X}<3-3 \sigma / 2)+P(\bar{X}>3+3 \sigma / 2).This probability is equal to 1/ ARL = 1/10 = 0.10 (see Figure 10.8). The process mean, 3.5, is closer to 3 + 3σ /2 than to 3 – 3σ /2. We will assume that the area to the left of 3 – 3σ /2 is negligible and that the area to the right of 3 + 3σ /2 is equal to 0.1 0. The z-score for 3 + 3σ /2 is then 1.28, so
\frac{(3+3 \sigma / 2)-3.5}{\sigma / 2}=1.28
Solving for σ, we obtain σ = 0.58. We finish by checking that the area to the left of 3-3σ /2 is negligible. Substituting σ = 0.58, we obtain 3 – 3σ /2 = 2.1 3. The z-score is (2 .1 3 – 3.5)/(0.58/2) = – 4.72. The area to the left of 3-3σ / 2 is indeed negligible.
