A ‘code converter’ is to be designed to convert from the BCD (5421) to the normal BCD (8421). The input BCD combinations for each digit are given below. A block diagram of the converter is shown in figure.
| Decimal | BCD (5421) | |||
| A | B | C | D | |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 0 | 1 |
| 7 | 1 | 0 | 1 | 0 |
| 8 | 1 | 0 | 1 | 1 |
| 9 | 1 | 1 | 0 | 0 |
(a) Draw K-maps for outputs W, X, Y and Z.
(b) Obtain minimized expression for the output W, X, Y and Z.
| Decimal | BCD(5421) | BCD(8421) | ||||||
| A | B | C | D | W | X | Y | Z | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 6 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 7 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 7 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 9 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
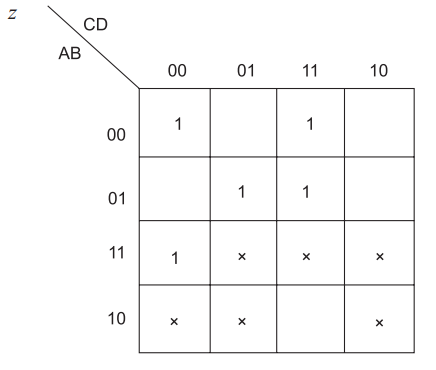
W = ∑m(11, 12) + ∑d(5, 6, 7, 13, 14, 15)
X = ∑m(4, 8, 9, 10) + ∑d(5, 6, 7, 13, 14, 15)
Y = ∑m(2, 3, 9, 10) + ∑d(5, 6, 7, 13, 14, 15)
Z = ∑m(1, 3, 8, 10, 12) + ∑d(5, 6, 7, 13, 14, 15)
(b) W = AB + ACD
X=\bar{A} B+A \bar{B} \bar{C}+A \bar{B} \bar{D}or
\bar{A} B+A \bar{B} \bar{C}+A C \bar{D}or
\begin{aligned}&\bar{A} B+A \bar{C} D+A \bar{B} \bar{D} \\&Y=\bar{A} C+A \bar{C} D+C \bar{D} \\&Z=\bar{A} D+A \bar{D}\end{aligned}(a)
| Decimal | BCD(5421) | BCD(8421) | ||||||
| A | B | C | D | W | X | Y | Z | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 9 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
W = ∑m(11, 12) + ∑d(8, 9, 10, 13, 14, 15)
X = ∑m(4, 5, 6, 7) + ∑d(8, 9, 10, 13, 14, 15)
Y = ∑m(2, 3, 6, 7) + ∑d(8, 9, 10, 13, 14, 15)
Z = ∑m(1, 3, 5, 7, 12) + ∑d(8, 9, 10, 13, 14, 15)
Hence, the correct option is (a).
