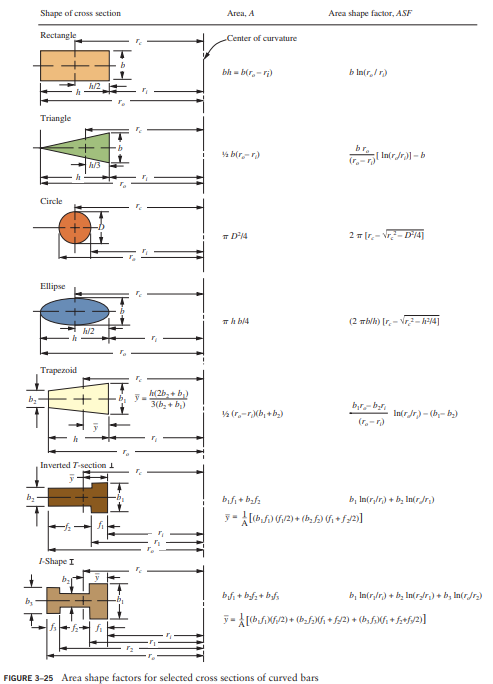
A curved bar has a rectangular cross section 15.0 mm thick by 25.0 mm deep as shown in Figure 3–26.
The bar is bent into a circular arc producing an inside radius of 25.0 mm. For an applied bending moment of +400 N . m, compute the maximum tensile and compressive stresses in the bar.
Objective: Compute the maximum tensile and compressive stresses.
Given: M = +400 N . m that tends to straighten the bar. r_i = 25.0 mm.
Analysis: Apply Equations (3–28) and (3–29).
\sigma_{o}=\frac{M\left(R-r_{o}\right)}{A r_{o}\left(r_{c}-R\right)} (3.28)
\sigma_{i}=\frac{M\left(R-r_{i}\right)}{A r_{i}\left(r_{c}-R\right)} (3.29)
Results: First compute the cross-sectional area:
A=b h=(15.0 \mathrm{~mm})(25.0 \mathrm{~mm})=375.0 \mathrm{~mm}^{2}
Now compute the quantities involving radii. See Figure 3-26 for related dimensions:
\begin{aligned}&r_{o}=r_{i}+h=25.0 \mathrm{~mm}+25.0 \mathrm{~mm}=50.0 \mathrm{~mm} \\&r_{c}=r_{i}+h / 2=25.0 \mathrm{~mm}+(25.0 / 2) \mathrm{mm}=37.5 \mathrm{~mm} \\&R=A / AS F\end{aligned}
From Figure 3-25, for a rectangular cross section:
A S F=b \cdot \ln \left(r_{0}/ r_{i}\right)=(15 \mathrm{~mm})[\ln (50.0 / 25.0)]=10.3972 \mathrm{~mm}
Then, R= A/ASF =\left(375 \mathrm{~mm}^{2}\right) / 10.3972 \mathrm{~mm}=36.0674 \mathrm{~mm} Quantities needed in the stress equations include:
r_{c}-R=37.5 \mathrm{~mm}-36.0674 \mathrm{~mm}=1.4326 \mathrm{~mm}
This is the distance e as shown in Figure 3-24.
\begin{aligned}R-r_{o} &=36.0674 \mathrm{~mm}-50.0 \mathrm{~mm}=-13.9326 \mathrm{~mm} \\R-r_{i} &=36.0674 \mathrm{~mm}-25.0 \mathrm{~mm}=11.0674 \mathrm{~mm}\end{aligned}
This is the distance from the inside surface to the neutral axis. Stress at outer surface, using Equation (3-28):
\begin{aligned}&\sigma_{o}=\frac{M\left(R-r_{o}\right)}{A r_{o}\left(r_{c}-R\right)}=\frac{(400 \mathrm{~N} \cdot \mathrm{m})(-13.9326 \mathrm{~mm})[1000 \mathrm{~mm} /\mathrm{m}]}{\left(375 \mathrm{~mm}^{2}\right)(50.0 \mathrm{~mm})(1.4326 \mathrm{~mm})} \\&\sigma_{0}=-207.5 \mathrm{~N} / \mathrm{mm}^{2}=-207.5 \mathrm{MPa}\end{aligned}
This is the maximum compressive stress in the bar.
Stress at inner surface, using Equation (3-29):
\begin{aligned} &\sigma_{i}=\frac{M\left(R-r_{i}\right)}{A r_{i}\left(r_{c}-R\right)}=\frac{(400 \mathrm{~N} \cdot \mathrm{m})(11.0674 \mathrm{~mm})[1000 \mathrm{~mm} / \mathrm{m}]}{\left(375 \mathrm{~mm}^{2}\right)(25.0 \mathrm{~mm})(1.4326 \mathrm{~mm})} \\&\sigma_{\mathrm{i}}=329.6 \mathrm{~N} / \mathrm{mm}^{2}=329.6 \mathrm{MPa}\end{aligned}
This is the maximum tensile stress in the bar.
Comment: The stress distribution between the outside and the inside is similar to that shown in Figure 3–24.
