Question 3.18: A curved beam has the shape shown in Figure 3–28 and is subj...

Objective: Compute the maximum tensile and compressive stresses.

Given: M = -640 lb . in that tends to decrease the radius of curvature.
r_i = 2.90 in (see Figure 3–28 for related dimensions).
Analysis: Apply Equations (3–28) and (3–29)

\sigma_{o}=\frac{M\left(R-r_{o}\right)}{A r_{o}\left(r_{c}-R\right)}                                (3.28)

\sigma_{i}=\frac{M\left(R-r_{i}\right)}{A r_{i}\left(r_{c}-R\right)}                                (3.29)

Results: Separate the shape into a composite of an inverted T-section 1 and a semicircular area 2. Compute cross-sectional area for each part:

\begin{aligned}&A_{1}=b_{1} f_{1}+b_{2} f_{2}=(0.80 \mathrm{in})(0.20 \mathrm{in})+(1.0\mathrm{in})(0.40 \mathrm{in}) \\&A_{1}=0.560 \mathrm{in}^{2} \\&A_{2}=\pi D^{2} /8=\pi(0.40 \mathrm{in})^{2} / 8=0.06283 \mathrm{in}^{2}\end{aligned}
Total area =A=A_{1}+A_{2}=0.560+0.06283=0.62283 \mathrm{in}^{2}
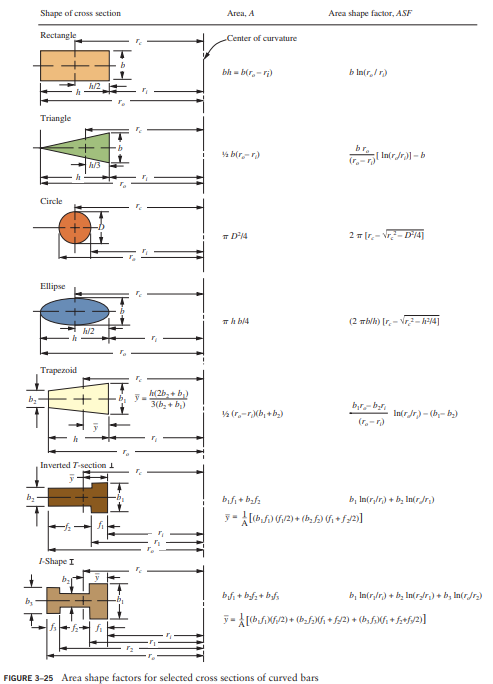
Now locate the centroid of each area with respect to the inside surface; from Figure 3-25:
\begin{aligned}&\bar{y}_{1}=\left[1 / A_{1}\right]\left[\left(b_{1} f_{1}\right)\left(f_{1} / 2\right)+\left(b_{2} f_{2}\right)\left(f_{1}+f_{2} / 2\right)\right] \\&\bar{y}_{1}=\left[1 / 0.56 \mathrm{in}^{2}\right][(0.80)(0.20)(0.10)+(1.0)(0.40)(0.70)]\mathrm{in}^{3} \\&\bar{y}_{1}=0.5286 \mathrm{in} \\&\bar{y}_{2}=1.20 \mathrm{in}+2\mathrm{D} / 3 \pi=1.20 \mathrm{in}+(2)(0.40 \mathrm{in}) /(3)(\pi) \\&\bar{y}_{2}=1.2849 \mathrm{in}\end{aligned}

Now locate the centroid of the composite area:
\begin{aligned}&\bar{y}_{c}=[1 / A]\left[A_{1} \bar{y}_{1}+A_{2} \bar{y}_{2}\right] \\&\bar{y}_{c}=\left[1 / 0.62283 \mathrm{in}^{2}\right][(0.560)(0.5286)+(0.06283)(1.2849)]\mathrm{in}^{3} \\&\bar{y}_{c}=0.60489 \mathrm{in}\end{aligned}
Now define the pertinent radii from the center of curvature:
\begin{aligned}&r_{o}=r_{i}+1.40 \text { in }=2.90 \text { in }+1.40 \text { in }=4.30\text { in } \\&r_{c}=r_{i}+\bar{y}_{c}=1.40 \text { in }+0.60489 \text { in }=3.5049 \text { in }\end{aligned}
Compute the value of the area shape factor, A S F_{\mathrm{i}}, for each part: For the T-shape:
\begin{aligned}&A S F_{1}=b_{1} \ln \left(r_{1} / r_{i}\right)+b_{2} \ln \left(r_{o 1} /r_{1}\right) \\&A S F_{1}=(0.80 \mathrm{in}) \ln (3.1 / 2.9)+(0.40 \mathrm{in}) \ln (4.1/3.1) \\&A S F_{1}=0.16519 \mathrm{in}\end{aligned}

For the semicircular area, we must determine the relationship between r_{i2} and D / 2 :
r_{i2}=4.10 \mathrm{in} at the base of the semicircle
D / 2=(0.40 \mathrm{in}) / 2=0.20 \mathrm{in}
Because r_{i2}>D / 2, we use the equation,
A S F_{2}=r_{i} \pi-D-\pi \sqrt{r_{i2}^{2}-D^{2} / 4}+2 \sqrt{r_{i2}^{2}-D^{2} / 4}\left[\sin ^{-1}\left(D / 2 r_{i}\right)\right]

[Note: Argument of inverse sine is in radians]
\begin{aligned}A S F_{2}=&(4.10) \pi-0.40-\pi \sqrt{(4.1)^{2}-(0.40)^{2} / 4} \\&+2\sqrt{(4.1)^{2}-(0.40)^{2} / 4}\left[\sin ^{-1}(0.40) /(2)(4.1)\right]=0.015016\mathrm{in}\end{aligned}
Compute the radius, R, from the center of curvature to the neutral axis from:
\begin{aligned}&R=A / \Sigma\left(A S F_{j}\right)=0.62283 \mathrm{in}^{2} /(0.16519+0.015016) \text { in } \\&R=3.4563 \text { in }\end{aligned}
Now compute:
\begin{aligned}r_{C}-R &=3.5049 \text { in }-3.4563 \text { in }=0.0486 \text { in }=e \\R-r_{o} &=3.4563 \text { in }-4.30 \text { in }=-0.8437 \text { in } \\R-r_{i} &=3.4563\text { in }-2.90 \text { in }=0.5563 \text { in }\end{aligned}

This locates the neutral axis from the inner surface.
Now compute the stress at outer surface, using Equation (3-28):
\begin{aligned}&\sigma_{o}=\frac{M\left(R-r_{o}\right)}{A r_{o}\left(r_{c}-R\right)}=\frac{(-640 \mathrm{lb} \cdot\mathrm{in})(-0.8437 \mathrm{in})}{\left(0.62283 \mathrm{in}^{2}\right)(4.30 \mathrm{in})(0.0486 \mathrm{in})} \\&\sigma_{o}=4149 \mathrm{lb} / \mathrm{in}^{2}=4149 \mathrm{psi}\end{aligned}
This is the maximum tensile stress in the bar.
Stress at inner surface, using Equation (3-29):
\begin{aligned}\sigma_{i} &=\frac{M\left(R-r_{j}\right)}{A r_{i}\left(r_{c}-R\right)}=\frac{(-640 \mathrm{lb} \cdot\mathrm{in})(0.5563 \mathrm{in})}{\left(0.62283 \mathrm{in}^{2}\right)(2.90 \mathrm{in})(0.0486 \mathrm{in})} \\\sigma_{\mathrm{i}}=-4056 \mathrm{lb} / \mathrm{in}^{2} &=-4056 \mathrm{psi}\end{aligned}
This is the maximum compressive stress in the bar.

Comment: This problem demonstrated the process for analyzing a composite section. Note that the maximum tensile and compressive stresses are very nearly equal for this design, a desirable condition for homogeneous, isotropic materials.