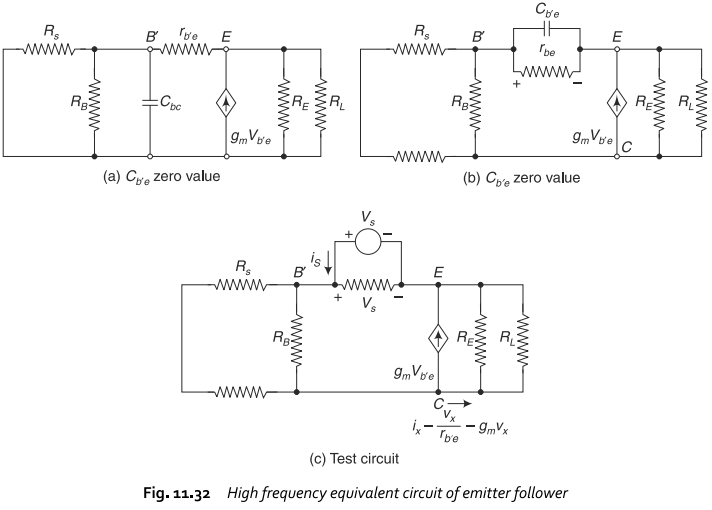
Calculate the high 3 dB cut-off frequency f_{H} of BJT Emitter follower as shown in Fig. 11.32, whose parameters are C_{b^{′}e} = 15 pF, C_{b^{′}c} = 1 pF, g_{m} = 57.14 m mho, β= 80, R_{s} = 200 Ω , r_{b^{′}e} = 1.4 kΩ .
Question 11.18: Calculate the high 3 dB cut-off frequency fH of BJT Emitter ...
The Blue Check Mark means that this solution has been answered and checked by an expert. This guarantees that the final answer is accurate.
Learn more on how we answer questions.
Learn more on how we answer questions.
R_{B} = R_{1} || R_{2}= 75 × 10^{3} || 4.35 × 10^{3} = 3.66 k \Omega
We know that f_{H}=\frac{1}{2\pi (R_{C_{b^{′}e}}C_{b^{′}e}+ R_{C_{b^{′}C}} C_{b^{′}C})}
where R_{C_{b^{′}e}}= r_{b^{′}e}\parallel \frac{R_{B}\parallel R_{s}+R_{L}\parallel R_{E} }{1+g_{m}(R_{L}\parallel R_{E} ) }
R_{C_{b^{′}C}}= (R_{B} || R_{s}) || [r_{b^{′}e} + (1 + \beta ) (R_{E} || R_{L})]
R_{C_{b^{′}C}} = (2.665 × 10^{3} || 200) || [1.45 × 10^{3} + (1 + 80) (330 || 55 × 10^{3})]
= 184.6 Ω
R_{C_{b^{′}e}}= 1.4\Omega \parallel \frac{(2.66 \times 10^{3}\parallel 200)+(5\times 10^{3}\parallel 330)}{1+57.14\times 10^{-3}\times (55\times 10^{3}\parallel 330)}
= 26.02 Ω
Hence, the 3 dB upper cut-off frequency is
f_{H}=\frac{1}{2\pi (R_{C_{b^{′}e}}C_{b^{′}e}+ R_{C_{b^{′}C}} C_{b^{′}C})}
=\frac{1}{2\pi (20.02\times 15\times 10^{-12} +184.6\times 1\times 10^{-12} )}
= 276.9 MHz
Related Answered Questions
(a) To determine dc bias values:
R_{B} = R_...
Voltage gain in dB = 20 \log_{10} ...
The lower 3 dB frequency, f_{1}=\frac{1}{2\...
We know that f_{T}=\beta f_{\beta }=\beta _...
f_{\alpha } \approx \frac{h_{fe}}{2\pi r_{b...
We know that f_{T}=\beta f_{\...
g_{m}=\frac{I_{C}(mA)}{26 mV}=\frac{1}{26}...