Question 6.13: Neglecting channel-length modulation and body effect, calcul...
Neglecting channel-length modulation and body effect, calculate the transfer function of the circuit shown in Fig. 6.27(a).

Learn more on how we answer questions.
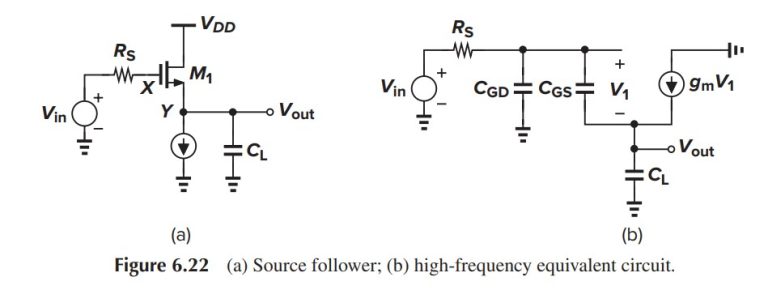
Let us first identify all of the capacitances in the circuit. At node X,C_{G D1} and C_{DB2} are connected to ground and C_{GS1} and C_{G D2} to Y . At node Y ,C_{SB1},C_{GS2}, and C_L are connected to ground. Similar to the source follower of Fig. 6.22(b), this circuit has three capacitances in a loop and hence a second-order transfer function. Using the equivalent circuit shown in Fig. 6.27(b), where C_X = C_{G D1} +C_{DB2}, C_{XY} = C_{GS1} +C_{G D2}, and C_Y = C_{SB1} +C_{GS2} +C_L , we have V_1C_{XY} s + g_{m1}V_1 = V_{out}C_Y s, and hence V_1 = V_{out}C_Y s/(C_{XY} s + g_{m1}). Also, since V_2 = V_{out}, the summation of currents at node X gives
(V_1 + V_{out})C_X s + g_{m2}V_{out} + V_1C_{XY} s = \frac{V_{in} − V_1 − V_{out}}{R_S} (6.61)
Substituting for V_1 and simplifying the result, we obtain
\frac{V_{out}}{V_{in}}(s)=\frac{g_{m1} + C_{XY} s}{R_Sξ s^2 + [C_Y + g_{m1}R_SC_X + (1 + g_{m2}R_S)C_{XY} ]s + g_{m1}(1 + g_{m2}R_S)} (6.62)
where ξ = C_XC_Y + C_XC_{XY} + C_YC_{XY} . As expected, (6.62) reduces to a form similar to (6.51) for g_{m2} = 0.