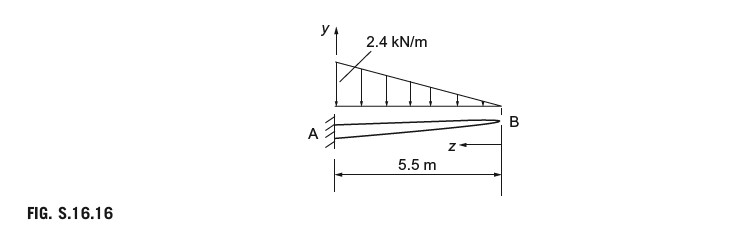
Question 16.16: For the aircraft at touchdown in P.14.1 calculate the deflec......
For the aircraft at touchdown in P.14.1 calculate the deflection of the wing tip relative to the section AA if the span of the wing outboard of AA is 5.5 m and the weight of this part of the wing is distributed linearly from zero at the tip to 2.4 kN/m at AA. Further, the second moment of area of the wing section reduces linearly from a value of 27.4\times10^{6}\,{\mathrm{mm}}^{4} at AA (see Example 16.4) to 2.4\times10^{6}\,{\mathrm{mm}}^{4} at the tip. Take Young’s modulus E = 70,000 N/mm².
Answer: 0.14 m.
The distribution of wing weight is shown in Fig. S.16.16. Then, at any section a distance z from the wing tip,
{\frac{w}{x}}={\frac{2.4}{5.5}}so that
w=0.44zThe bending moment due to the self-weight of the wing at any section a distance z from the wing tip is then
M_{z}(\mathrm{self-wt})={\frac{1}{2}}\times0.44z^{2}\times{\frac{z}{3}}=0.073z^{3}The bending moment due to the deceleration at touch-down at any section is then
M_{z}(\mathrm{decel})=0.073\times1.96z^{3}=0.143z^{3}\;{\mathrm{(see~S.14.1)}}The total bending moment due to self-weight and deceleration is therefore
M_{z}(\mathrm{total})=0.216z^{3}The second moment of area of the wing sections is given by
I=\left(2.4+\frac{z}{5.5}\times25\right)\times10^{6}=(2.4+4.55z)\times10^{6}Using the moment-area method and taking the origin for z at B (see Fig. S.16.16), \nu_{\mathrm{{A}}}=(\mathrm{{d}}\nu/\mathrm{d}z)_{\mathrm{A}}=z_{\mathrm{B}}=0. Equation (16.33) then reduces to
z_{\mathrm{B}}\left({\frac{\mathrm{d}\nu}{\mathrm{d}z}}\right)_{\mathrm{B}}-z_{\mathrm{A}}\left({\frac{\mathrm{d}\nu}{\mathrm{d}z}}\right)_{\mathrm{A}}-\left(\nu_{\mathrm{B}}-\nu_{\mathrm{A}}\right)=-\int_{\mathrm{A}}^{\mathrm{B}}{\frac{M}{EI}}z\,\mathrm{d}z (16.33)
v_{B}=-\int_{0}^{5.5}{\frac{M_{z}}{EI}z } dz
Substituting for M_{z}, etc., from the above,
\nu_{\mathrm{B}}=-{\frac{1}{E}}{\int_{0}^{5.5}{\displaystyle{\frac{0.216z^{4}}{10^{6}(2.4+4.55z)/10^{12}}}}}\mathrm{d}zwhich simplifies to
\nu_{\mathrm{B}}=-{\frac{0.68}{10^{3}}}{\int_{0}^{5.5}{\frac{z^{4}}{(0.53+z)}}\,\mathrm{d}z}The integral may be evaluated by expressing it as two parts that are obtained by dividing the numerator by the denominator using the normal rules of algebraic division. Then
that is,
which gives
\nu_{\mathrm{B}}=-0.14\,\mathrm{m} (downwards)
