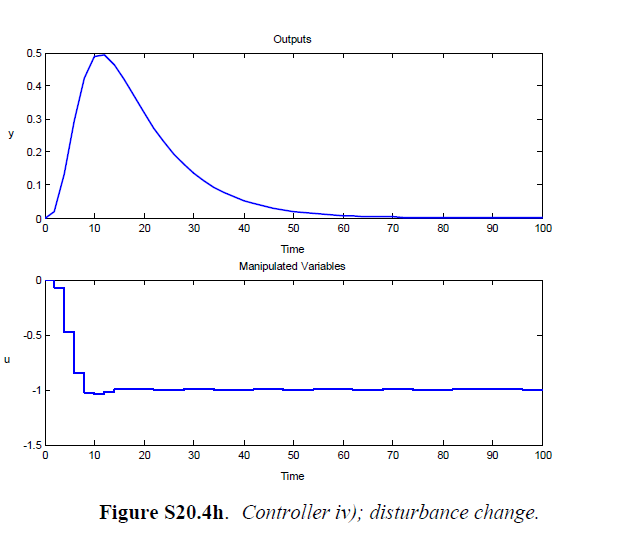
Consider the transfer function model of Exercise 20.1. For each of the four sets of design parameters shown below, design a model predictive controller. Then do the following:
(a) Compare the controllers for a unit step change in set point. Consider both the y and u responses.
(b) Repeat the comparison of (a) for a unit step change in disturbance, assuming that G_{d}(s)=G(s).
(c) Which controller provides the best performance? Justify your answer.
| Set No. | Δt | N | M | P | R |
| (i) | 2 | 40 | 1 | 5 | 0 |
| (ii) | 2 | 40 | 20 | 20 | 0 |
| (iii) | 2 | 40 | 3 | 10 | 0.01 |
| (iv) | 2 | 40 | 3 | 10 | 0.1 |