Question 9.8: A compound beam ABC has a roller support at A, an internal h......
A compound beam ABC has a roller support at A, an internal hinge (that is, moment release) at B, and a fixed support at C (Fig. 9-20a). Segment AB has a length of a and segment BC has a length of b. A concentrated load P acts at a distance 2a/3 from support A, and a uniform load of intensity q acts between points B and C.
Determine the deflection δ_B at the hinge and the angle of rotation θ_A at support A (Fig. 9-20d). Note: The beam has constant flexural rigidity EI.


Learn more on how do we answer questions.
Use a four-step problem-solving approach.
1. Conceptualize: For purposes of analysis, consider the compound beam to consist of two individual beams: a simple beam AB of length a and a cantilever beam BC of length b. The two beams are linked together by a pin connection at B.
2. Categorize: If you separate beam AB from the rest of the structure (Fig. 9-20b), there is a vertical force F at end B equal to 2P/3. This same force acts downward at end B of the cantilever (Fig. 9-20c). Consequently, the cantilever beam BC is subjected to two loads: a uniform load and a concentrated load.
3. Analyze: The deflection at the end of this cantilever (which is the same as the deflection δ_B of the hinge) is readily found from Cases 1 and 4 of Table H-1, Appendix H:
\quad\quad\quad\quad \delta_{E}=\frac{q b^{4}}{8E I}+\frac{F b^{3}}{3E I}
or, since F = 2P / 3,
\quad\quad\quad\quad\delta_{B}=\frac{q b^{4}}{8E I}+\frac{2P b^{3}}{9_{E I}}\quad\quad (9-65)
The angle of rotation θ_A at support A (Fig. 9-20d) consists of two parts: an angle BAB’ produced by the downward displacement of the hinge and an additional angle of rotation produced by the bending of beam AB (or beam AB’) as a simple beam. The angle BAB’ is
\quad\quad\quad\quad (\theta_{A})_{1}={\frac{\delta_{B}}{\alpha}}={\frac{q b^{4}}{8\alpha E I}}+{\frac{2P b^{3}}{9\alpha E I}}
The angle of rotation at the end of a simple beam with a concentrated load is obtained from Case 5 of Table H-2. The formula given there is
\quad\quad\quad\quad \frac{P a b(L+b)}{6L E I}
in which L is the length of the simple beam, a is the distance from the left-hand support to the load, and b is the distance from the right-hand support to the load. Thus, in the notation of this example (Fig. 9-20a), the angle of rotation is
\quad\quad\quad\quad (\theta_{A})_{2}={\frac{{ P}{\Bigg\lgroup}{\frac{2\alpha}{3}}{\Bigg\rgroup}{\Bigg\lgroup}{\frac{\alpha}{3}}{\Bigg\rgroup}{\Bigg\lgroup}{\alpha}+{\frac{\alpha}{3}}{\Bigg\rgroup}}{6\alpha E I}}={\frac{4{P}\alpha^{2}}{81EI}}
Combine the two angles to obtain the total angle of rotation at support A:
\quad\quad\quad\quad\theta_{A}=(\theta_{A})_{1}+(\theta_{A})_{2}=\frac{qb^{4}}{8\alpha E I}+\frac{2P b^{3}}{9\alpha E I}+\frac{4P\alpha^{2}}{81E I}
4. Finalize: This example illustrates how the method of superposition can be adapted to handle a seemingly complex situation in a relatively simple manner.
| Table H-1 | |
| Deflections and Slopes of Cantilever Beams | |
 |
Notation: v = deflection in the y direction (positive upward) v’ = dv/dx = slope of the deflection curve δ_B = -v(L) = deflection at end B of the beam (positive downward) θ_B = -v'(L) = angle of rotation at end B of the beam (positive clockwise) EI = constant |
 |
\nu=-{\frac{q x^{2}}{24E I}}(6L^{2}-4L x+x^{2})\quad\quad v' = {\frac{q x}{6E I}}(3L^{2} – 3 L x+x^{2}) \\ δ_B = {\frac{q L^4}{8E I}} \quad \theta_B = {\frac{q L^3}{6E I}} |
 |
\displaystyle{v=-\frac{q x^{2}}{24E I}(6a^{2}-4\alpha x+x^{2})}\qquad\qquad(0\leq x\leq a) \\ \displaystyle{v'=-\frac{q x}{6E I}(3a^{2}- 3\alpha x+x^{2})}\qquad\qquad(0\leq x\leq a) \\ \displaystyle{v=-\frac{q a^{3}}{24E I}(4x – a)} \quad\quad \displaystyle{v'=-\frac{q a^{3}}{6E I}}\qquad(a\leq x\leq L) \\ At \, x= a : v = -\frac{q a^{4}}{8E I} \quad v' = -\frac{q a^{3}}{6E I}\\ \delta_B = {\frac{q a^{3}}{24E I}(4L – a)}\quad \theta_B = \frac{q a^{3}}{6E I} |
 |
\displaystyle{v=-\frac{qb x^{2}}{12E I}(6L+3\alpha – 2x)}\qquad\qquad(0\leq x\leq a) \\ \displaystyle{v'= -\frac{qb x}{2E I}(L+ \alpha – x)}\qquad\qquad(0\leq x\leq a) \\ \displaystyle{v=-\frac{q }{24E I}(x^4 -4Lx^3 +6L^2x^2 – 4a^3x + a^4)} \qquad\qquad(a\leq x\leq L) \\ \displaystyle{v'=-\frac{q }{6E I}(x^3 -3Lx^2 + 3L^2x – a^3)} \qquad\qquad(a\leq x\leq L)\\ AT x = a: \, v = -\frac{qa^2b}{12EI}(3L + a) \quad v' = -\frac{qabL}{2EI}\\ \delta_B = {\frac{q }{24E I}(3L^4 -4 a^3L + a^4)}\quad \theta_B = \frac{q }{6E I}(L^3 – a^3) |
 |
v = -\frac{Px^2}{6EI}(3L – x) \quad v' = -\frac{Px}{2EI}(2L – x)\\ \delta_B = {\frac{PL^3}{3E I}}\quad \theta_B = \frac{PL^2}{2E I} |
 |
\displaystyle{v=-\frac{Px^{2}}{6E I}(3a – x)}\quad \displaystyle{v'=-\frac{Px}{2E I}(2a- x)}\qquad\qquad(0\leq x\leq a) \\ \displaystyle{v=-\frac{Pa^{2}}{6E I}(3x – a)} \quad\quad \displaystyle{v'=-\frac{Pa^{2}}{2E I}}\qquad(a\leq x\leq L) \\ At \, x= a : v = -\frac{Pa^{3}}{3E I} \quad v' = -\frac{Pa^{2}}{2E I}\\ \delta_B = {\frac{P a^{2}}{6E I}(3L – a)}\quad \theta_B = \frac{P a^{2}}{2E I} |
 |
\nu=-\frac{M_{o}x^{2}}{2E I}\quad\quad \nu^{\prime}=-\frac{M_{o}x}{E I} \\ \delta_B=-\frac{M_{o}L^{2}}{2E I}\quad\quad \theta_{B}=-\frac{M_{o}L}{E I} |
 |
\displaystyle{v=-\frac{M_o x^{2}}{2E I}}\qquad \displaystyle{v'=-\frac{M_o x}{E I}}\qquad(0\leq x\leq a) \\ \displaystyle{v=-\frac{M_o a}{2E I}}(2x – a) \quad \displaystyle{v'=-\frac{M_o a}{E I}}\qquad(0\leq x\leq a) \\ At \, x= a : \displaystyle{v=-\frac{M_o a^{2}}{2E I}}\qquad \displaystyle{v'=-\frac{M_o a}{E I}}\\ \delta_B = {\frac{M_o a}{2E I}(2L – a)}\quad \theta_B = \frac{M_o a}{E I} |
 |
\displaystyle{v=-\frac{q_o x^{2}}{120LE I}(10L^{3} – 10L^2 x + 5Lx^{2} – x^3)} \\ \displaystyle{v'=-\frac{q_o x}{24LE I}(4L^{3}- 6L^2 x + 4Lx^{2} – x^3)} \\ \delta_B = {\frac{q_o L^{4}}{30E I}}\quad \theta_B = \frac{q_o L^{3}}{24E I} |
 |
\displaystyle{v=-\frac{q_o x^{2}}{120LE I}(20L^{3} – 10L^2 x + x^3)} \\ \displaystyle{v'=-\frac{q_o x}{24LE I}(8L^{3}- 6L^2 x + x^3)} \\ \delta_B = {\frac{11q_o L^{4}}{120E I}}\quad \theta_B = \frac{q_o L^{3}}{8E I} |
 |
\displaystyle{v=-\frac{q_o L}{3\pi ^4E I}(48L^{3}\cos {\frac{\pi x}{2L}} – 48L^3 + 3\pi ^3Lx^2 – \pi^3x^3)} \\ \displaystyle{v'=-\frac{q_o L}{\pi ^3E I}( 2\pi ^2Lx – \pi^2x^2 – 8L^{2}\sin {\frac{\pi x}{2L}})} \\ \delta_B = {\frac{2q_o L^{4}}{3\pi^4E I}}(\pi^3 – 24)\quad \theta_B = \frac{q_o L^{3}}{\pi^3E I}(\pi^2 – 8) |
| Table H-2 | |
| Deflections and Slopes of Cantilever Beams | |
 |
Notation: v = deflection in the y direction (positive upward) v’ = dv/dx = slope of the deflection curve δ_C = -v(L/2) = deflection at end B of the beam (positive downward) x_1 = distance from support A to point of maximum deflection \delta_{max} = -v_{max} = maximum deflection (positive downward) \theta_A = -v'(0) = angle of rotation at left-hand end of the beam (positive clockwise) \theta_B = v'(L) = angle of rotation at right-hand end of the beam (positive counterclockwise) EI = constant |
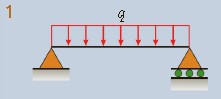 |
\begin{array}{l}{{\nu=-{\frac{q x}{24E I}}(L^{3}-2L x^{2}+x^{3})}}\\ {{\nu'=-{\frac{q}{24E I}}(L^{3}-6L x^{2}+4x^{3})}}\\ {{\mathrm{~\delta_{C}= \delta_{max}= -\frac{5qL^4}{384E I} \quad \theta_A = \theta_B = \frac{qL^3}{24EI}}}}\end{array} |
 |
\begin{array}{l}{{\nu=-{\frac{q x}{384E I}}(9L^{3} – 24L x^{2} + 16x^{3})}} \quad\quad \left(0\leq x\leq{\frac{L}{2}}\right) \\ {{\nu'=-{\frac{q}{384E I}}(9L^{3} – 72L x^{2} + 64x^{3})}}\quad\quad \left(0\leq x\leq{\frac{L}{2}}\right) \\ \nu=-{\frac{q L}{384E I}}(8x^{3} – 24L x^{2} + 17L^{2}x – L^3) \quad\quad \left(\frac{L}{2}\leq x\leq {L}\right) \\ \nu'=-{\frac{q L}{384E I}}(24x^{2} – 48L x + 17L^{2}) \quad\quad \left(\frac{L}{2}\leq x\leq {L}\right) \\ {{\mathrm{~\delta_{C}= -\frac{5qL^4}{768E I} \, \theta_A = \frac{3qL^3}{128EI} \, \theta_B = \frac{7qL^3}{384EI}}}} \end{array} |
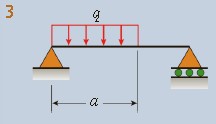 |
\begin{array}{l}{{\nu=-{\frac{q x}{24LE I}}(a^{4} – 4a^3L +4a^2L^2 + 2a^2x^2 – 4aLx^2 + Lx^{3})}} \quad\quad (0 \leq x \leq a)\\ {{\nu'=-{\frac{q}{24LE I}}(a^{4} – 4a^3L +6a^2L^2 + 6a^2x^2 – 12aLx^2 – 4Lx^{3})}} \quad\quad (0 \leq x \leq a) \\ \nu=-{\frac{q a^2}{24LE I}}(-a^{2}L + 4L^{2}x + a^2 x -6 Lx^2 + 2x^3) \quad\quad (a \leq x \leq {L})\\ \nu'=-{\frac{q A^2}{24LE I}}(4L^{2} + a^2 – 12Lx + 6x^2) \quad\quad\quad\quad (a \leq x \leq {L}) \\ {{\mathrm{~ \theta_A = \frac{qa^2}{24LEI}(2L – a)^2 \, \theta_B = \frac{qa^2}{24LEI}(2L^2 – a^2)}}} \end{array} |
 |
v=-{\frac{P x}{48E I}}(3L^{2}-4x^{2})\;\;\;\;\;v^{\prime}=-{\frac{P}{16E I}}(L^{2}-4x^{2})\;\;\;\;\left(0\leq x\leq{\frac{L}{2}}\right) \\ \delta_C = \delta_{max} = {\frac{PL^3}{48E I}}\quad\quad \theta_A = \theta_B = {\frac{PL^2}{16E I}} |
 |
\nu=-{\frac{P b x}{6L E I}}(L^{2}\,-\,b^{2}\,-\,x^{2}\,)\quad\nu^{\prime}=-{\frac{P b}{6L E I}}(L^{2}\,-\,b^{2}\,-\,3x^{2}\,)\quad(0\leq\,x\leq a) \\ \theta_A = \frac{Pab(L + a)}{6LEI} \quad \theta_B = \frac{Pab(L + a)}{6LEI} \\ If \, a ≥ b,\quad \delta_C = \frac{Pb(3L^2 – 4b^2)}{48EI} \quad If \, a \leq b,\quad \delta_C = \frac{Pa(3L^2 – 4a^2)}{48EI} \\ If \, a ≥ b,\quad x_1 = \sqrt{\frac{L^2 – b^2}{3}} \quad\quad and \quad \delta_{max}= \frac{Pb(L^2 – b^2)^{3/2}}{9\sqrt{3}LEI} |
 |
v=-{\frac{P x}{6E I}}(3aL – 3a^{2} – x^2)\;\;\;\;\;v^{\prime}=-{\frac{P}{2E I}}(aL – a^{2} – x^{2})\;\;\;\;\left(0\leq x\leq a\right) \\ v=-{\frac{P a}{6E I}}(3Lx – 3x^{2} – a^2)\;\;\;\;\;v^{\prime}=-{\frac{Pa}{2E I}}(L – 2 x)\;\;\;\;\left(a\leq x\leq L – a\right) \\ \delta_C = \delta_{max} = {\frac{Pa}{24E I}}(3L^2 – 4a^2)\quad\quad \theta_A = \theta_B = {\frac{P a (L- a)}{2E I}} |
 |
\nu=-\frac{M_{0}x}{6 LE I}(2L^{2} – 3L x + x^{2}) \quad {\nu}^{\prime}=-\frac{M_{0}}{6L E I}(2L^{2}-6L x+3x^{2}) \\ \delta_C = \frac{M_{0}L^2}{16 E I} \quad \theta_A = \frac{M_oL}{3EI} \quad \theta_B = \frac{M_o L}{6EI} \\ x_1 = L {{\Bigg\lgroup}}1 – \frac{\sqrt{3}}{3} {{\Bigg\rgroup}} \quad and \quad \delta_{max} = \frac{M_o L^2}{9\sqrt{3}EI} |
 |
\nu=-\frac{M_{0}x}{24 LE I}(L^{2} – 4x^{2}) \quad {\nu}^{\prime}=-\frac{M_{0}}{24L E I}(L^{2}-12x^{2}) \quad \left(0 \leq x \leq \frac{L}{2} \right) \\ \delta_C = 0 \quad \theta_A = \frac{M_oL}{24EI} \quad \theta_B = \frac{M_o L}{24EI} |
 |
\displaystyle{v=-\frac{M_o x}{6LE I}}(6aL – 3a^2 – 2 L^2 – x^2)\qquad(0\leq x\leq a) \\ \displaystyle{v'=-\frac{M_o }{6LE I}}(6aL – 3a^2 – 2 L^2 – 3x^2)\qquad(0\leq x\leq a) \\ At \, x= a : \displaystyle{v=-\frac{M_o ab}{3LE I}}(2a – L)\qquad \displaystyle{v'=-\frac{M_o }{3LE I}}(3aL – 3a^2 – L^2)\\ \theta_A = {\frac{M_o }{6LE I}(6 a L – 3a^2 – 2L^2)}\quad \theta_B = \frac{M_o }{6LE I}(3a^2 – L^2) |
 |
\nu=-\frac{M_{0}x}{2E I}(L – x ) \quad {\nu}^{\prime}=-\frac{M_{0}}{2 E I}(L – 2 x) \\ \delta_C = \delta_{max} = \frac{M_{0}L^2}{8 E I} \quad \theta_A = \theta_B = \frac{M_o L}{2EI} |
 |
\displaystyle{v=-\frac{q_o x}{360LE I}(7L^{4} – 10L^2 x^2 + 3Lx^{4} )} \\ \displaystyle{v'=-\frac{q_o }{360LE I}(7L^{4} – 30L^2 x^2 + 15x^{4} )} \\ \delta_C = {\frac{5q_o L^{4}}{768E I}}\quad \theta_A = \frac{7q_o L^{3}}{360E I} \quad \theta_B = \frac{q_o L^{3}}{45E I} \\ x_1 = 0.5193 L \quad \delta_{max} = 0.00652\frac{q_oL^4}{EI} |
 |
\displaystyle{v=-\frac{q_o x}{960LE I}(5L^2 – 4x^2)^2} \quad\quad \left( 0 \leq x \leq \frac{L}{2}\right) \\ \displaystyle{v'=-\frac{q_o}{192LE I}(5L^2 – 4x^2)(L^2 – 4x^2)} \quad\quad \left( 0 \leq x \leq \frac{L}{2}\right) \\ \delta_C = \delta_{max} = {\frac{q_o L^{4}}{120E I}} \quad \theta_A = \theta_B = \frac{5q_o L^{3}}{192E I} |
 |
\displaystyle{v=-\frac{q_o L^4}{\pi ^4E I}\sin {\frac{\pi x}{L}}} \quad \displaystyle{v'=-\frac{q_o L^3}{\pi ^3E I}\cos {\frac{\pi x}{L}}} \\ \delta_C = \delta_{max} = {\frac{q_o L^{4}}{\pi^4E I}} \quad \theta_A = \theta_B = \frac{q_o L^{3}}{\pi^3E I} |