Question 9.9: A simple beam AB of a span length L has an overhang BC of le......
A simple beam AB of a span length L has an overhang BC of length a (Fig. 9-21a).
The beam supports a uniform load of intensity q throughout its length.
Obtain a formula for the deflection δ_C at the end of the overhang (Fig. 9-21c).
Note: The beam has constant flexural rigidity EI.



Learn more on how do we answer questions.
Use a four-step problem-solving approach.
1. Conceptualize: Find the deflection of point C by imagining the overhang BC (Fig. 9-21a) to be a cantilever beam subjected to two actions. The first action is the rotation of the support of the cantilever through an angle \theta_B, which is the angle of rotation of beam ABC at support B (Fig. 9-21c). (Assume that a clockwise angle \theta_B is positive.) This angle of rotation causes a rigid-body rotation of the overhang BC, resulting in a downward displacement \delta_1 of point C.
The second action is the bending of BC as a cantilever beam supporting a uniform load. This bending produces an additional downward displacement \delta_2 (Fig. 9-21c). The superposition of these two displacements gives the total displacement \delta_C at point C.
2. Categorize:
Deflection \delta_1: Begin by finding the deflection \delta_1 caused by the angle of rotation \theta_B at point B. To find this angle, observe that part AB of the beam is in the same condition as a simple beam (Fig. 9-21b) subjected to the following loads: a uniform load of intensity q, a couple M_B (equal to qa^2 / 2), and a vertical load P (equal to qa). Only the loads q and M_B produce angles of rotation at end B of this simple beam. These angles are found from Cases 1 and 7 of Table H-2, Appendix H. Thus, the angle \theta_B is
\quad\quad\quad\quad\theta_{B}=-{\frac{q L^{3}}{24E I}}+{\frac{M_{B}L}{3E I}}=-{\frac{q{L}^{3}}{24{E}I}}+{\frac{q a^{2}{L}}{6{E}I}}={\frac{q{L}(4 a^{2}-{L}^{2})}{24{E}{I}}}\quad\quad (9-67)
in which a clockwise angle is positive, as shown in Fig. 9-21c.
The downward deflection \delta_1 of point C, due solely to the angle of rotation \theta_B, is equal to the length of the overhang times the angle (Fig. 9-21c):
\quad\quad\quad\quad\delta_{1}=a\theta_{_{ B}}\,=\,\frac{q a{L}(4a^{2}-{L}^{2})}{24{ E}{ L}}\quad\quad (a)
Deflection δ_2: Bending of the overhang BC produces an additional downward deflection δ_2 at point C. This deflection is equal to the deflection of a cantilever beam of length a subjected to a uniform load of intensity q (see Case 1 of Table H-1):
\quad\quad\quad\quad{\delta}_{2}={\frac{q a^{4}}{8E I}}\quad\quad\quad\quad (b)
3. Analyze:
Deflection \delta_C: The total downward deflection of point C is the algebraic sum of \delta_1 ~ and ~ \delta_2:
\quad\quad\quad\quad\delta_{C}=\delta_{1}+\delta_{2}={\frac{q a{L}(4a^{2}-{L}^{2})}{24E I}}+{\frac{q a^{4}}{8E I}}={\frac{q a}{24E I}}[{L}(4a^{2} – {L}^{2})+3 a^{3}]
or
\quad\quad\quad\quad\delta_{C}={\frac{q a}{24E I}}(a+{L})(3a^{2}+a L- {L}^{2})\quad\quad (9-68)
4. Finalize: In the preceding equation, the deflection \delta_C may be upward or downward, depending upon the relative magnitudes of the lengths L and a. If a is relatively large, the last term in the equation (the three-term expression in parentheses) is positive, and the deflection \delta_C is downward. If a is relatively small, the last term is negative, and the deflection is upward. The deflection is zero when the last term is equal to zero:
\quad\quad\quad\quad 3a^{2}+a {L} – {L}^{2} = {0}
or
\quad\quad\quad\quad a={\frac{{L}\Big(\sqrt{13}\,-\,1\Big)}{6}}=0.434{{3L}}\quad\quad(c)
From this result, note that if a is greater than 0.4343L, the deflection of point C is downward; if a is less than 0.4343L, the deflection is upward.
Deflection curve: The shape of the deflection curve for the beam in this example is shown in Fig. 9-21c for the case where a is large enough (a > 0.4343L) to produce a downward deflection at C and small enough (a < L) to ensure that the reaction at A is upward. Under these conditions, the beam has a positive bending moment between support A and a point such as D. The deflection curve in region AD is concave upward (positive curvature). From D to C, the bending moment is negative; therefore, the deflection curve is concave downward (negative curvature).
Point of inflection: At point D, the curvature of the deflection curve is zero because the bending moment is zero. A point such as D, where the curvature and bending moment change signs, is called a point of inflection (or point of contraflexure). The bending moment M and the second derivative d^2v / dx^2 always vanish at an inflection point.
However, a point where M and d^2v / dx^2 equal zero is not necessarily an inflection point because it is possible for those quantities to be zero without changing signs at that point; for example, they could have maximum or minimum values.
| Table H-2 | |
| Deflections and Slopes of Simple Beams | |
 |
Notation: v = deflection in the y direction (positive upward) v’ = dv/dx = slope of the deflection curve δ_C = -v(L/2) = deflection at end B of the beam (positive downward) x_1 = distance from support A to point of maximum deflection \delta_{max} = -v_{max} = maximum deflection (positive downward) \theta_A = -v^\prime(0) = angle of rotation at left-hand end of the beam (positive clockwise) \theta_B = v^\prime(L) = angle of rotation at right-hand end of the beam (positive counterclockwise) EI = constant |
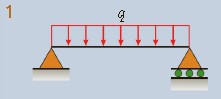 |
\begin{array}{l}{{\nu=-{\frac{q x}{24E I}}(L^{3}-2L x^{2}+x^{3})}}\\ {{\nu^\prime=-{\frac{q}{24E I}}(L^{3}-6L x^{2}+4x^{3})}}\\ {{\mathrm{~\delta_{C}= \delta_{max}= -\frac{5qL^4}{384E I} \quad \theta_A = \theta_B = \frac{qL^3}{24EI}}}}\end{array} |
 |
\begin{array}{l}{{\nu=-{\frac{q x}{384E I}}(9L^{3} – 24L x^{2} + 16x^{3})}} \quad\quad \left(0\leq x\leq{\frac{L}{2}}\right) \\ {{\nu^\prime=-{\frac{q}{384E I}}(9L^{3} – 72L x^{2} + 64x^{3})}}\quad\quad \left(0\leq x\leq{\frac{L}{2}}\right) \\ \nu=-{\frac{q L}{384E I}}(8x^{3} – 24L x^{2} + 17L^{2}x – L^3) \quad\quad \left(\frac{L}{2}\leq x\leq {L}\right) \\ \nu^\prime=-{\frac{q L}{384E I}}(24x^{2} – 48L x + 17L^{2}) \quad\quad \left(\frac{L}{2}\leq x\leq {L}\right) \\ {{\mathrm{~\delta_{C}= -\frac{5qL^4}{768E I} \, \theta_A = \frac{3qL^3}{128EI} \, \theta_B = \frac{7qL^3}{384EI}}}} \end{array} |
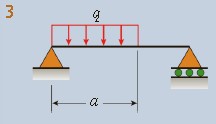 |
\begin{array}{l}{{\nu=-{\frac{q x}{24LE I}}(a^{4} – 4a^3L +4a^2L^2 + 2a^2x^2 – 4aLx^2 + Lx^{3})}} \quad\quad (0 \leq x \leq a)\\ {{\nu^\prime=-{\frac{q}{24LE I}}(a^{4} – 4a^3L +6a^2L^2 + 6a^2x^2 – 12aLx^2 – 4Lx^{3})}} \quad\quad (0 \leq x \leq a) \\ \nu=-{\frac{q a^2}{24LE I}}(-a^{2}L + 4L^{2}x + a^2 x -6 Lx^2 + 2x^3) \quad\quad (a \leq x \leq {L})\\ \nu^\prime=-{\frac{q A^2}{24LE I}}(4L^{2} + a^2 – 12Lx + 6x^2) \quad\quad\quad\quad (a \leq x \leq {L}) \\ {{\mathrm{~ \theta_A = \frac{qa^2}{24LEI}(2L – a)^2 \, \theta_B = \frac{qa^2}{24LEI}(2L^2 – a^2)}}} \end{array} |
 |
v=-{\frac{P x}{48E I}}(3L^{2}-4x^{2})\;\;\;\;\;v^{\prime}=-{\frac{P}{16E I}}(L^{2}-4x^{2})\;\;\;\;\left(0\leq x\leq{\frac{L}{2}}\right) \\ \delta_C = \delta_{max} = {\frac{PL^3}{48E I}}\quad\quad \theta_A = \theta_B = {\frac{PL^2}{16E I}} |
 |
\nu=-{\frac{P b x}{6L E I}}(L^{2}\,-\,b^{2}\,-\,x^{2}\,)\quad\nu^{\prime}=-{\frac{P b}{6L E I}}(L^{2}\,-\,b^{2}\,-\,3x^{2}\,)\quad(0\leq\,x\leq a) \\ \theta_A = \frac{Pab(L + a)}{6LEI} \quad \theta_B = \frac{Pab(L + a)}{6LEI} \\ If \, a ≥ b,\quad \delta_C = \frac{Pb(3L^2 – 4b^2)}{48EI} \quad If \, a \leq b,\quad \delta_C = \frac{Pa(3L^2 – 4a^2)}{48EI} \\ If \, a ≥ b,\quad x_1 = \sqrt{\frac{L^2 – b^2}{3}} \quad\quad and \quad \delta_{max}= \frac{Pb(L^2 – b^2)^{3/2}}{9\sqrt{3}LEI} |
 |
v=-{\frac{P x}{6E I}}(3aL – 3a^{2} – x^2)\;\;\;\;\;v^{\prime}=-{\frac{P}{2E I}}(aL – a^{2} – x^{2})\;\;\;\;\left(0\leq x\leq a\right) \\ v=-{\frac{P a}{6E I}}(3Lx – 3x^{2} – a^2)\;\;\;\;\;v^{\prime}=-{\frac{Pa}{2E I}}(L – 2 x)\;\;\;\;\left(a\leq x\leq L – a\right) \\ \delta_C = \delta_{max} = {\frac{Pa}{24E I}}(3L^2 – 4a^2)\quad\quad \theta_A = \theta_B = {\frac{P a (L- a)}{2E I}} |
 |
\nu=-\frac{M_{0}x}{6 LE I}(2L^{2} – 3L x + x^{2}) \quad {\nu}^{\prime}=-\frac{M_{0}}{6L E I}(2L^{2}-6L x+3x^{2}) \\ \delta_C = \frac{M_{0}L^2}{16 E I} \quad \theta_A = \frac{M_0L}{3EI} \quad \theta_B = \frac{M_0 L}{6EI} \\ x_1 = L {{\Bigg\lgroup}}1 – \frac{\sqrt{3}}{3} {{\Bigg\rgroup}} \quad and \quad \delta_{max} = \frac{M_0 L^2}{9\sqrt{3}EI} |
 |
\nu=-\frac{M_{0}x}{24 LE I}(L^{2} – 4x^{2}) \quad {\nu}^{\prime}=-\frac{M_{0}}{24L E I}(L^{2}-12x^{2}) \quad \left(0 \leq x \leq \frac{L}{2} \right) \\ \delta_C = 0 \quad \theta_A = \frac{M_oL}{24EI} \quad \theta_B = \frac{M_0 L}{24EI} |
 |
\displaystyle{v=-\frac{M_0 x}{6LE I}}(6aL – 3a^2 – 2 L^2 – x^2)\qquad(0\leq x\leq a) \\ \displaystyle{v^\prime=-\frac{M_0 }{6LE I}}(6aL – 3a^2 – 2 L^2 – 3x^2)\qquad(0\leq x\leq a) \\ At \, x= a : \displaystyle{v=-\frac{M_0 ab}{3LE I}}(2a – L)\qquad \displaystyle{v^\prime=-\frac{M_0 }{3LE I}}(3aL – 3a^2 – L^2)\\ \theta_A = {\frac{M_0 }{6LE I}(6 a L – 3a^2 – 2L^2)}\quad \theta_B = \frac{M_0 }{6LE I}(3a^2 – L^2) |
 |
\nu=-\frac{M_{0}x}{2E I}(L – x ) \quad {\nu}^{\prime}=-\frac{M_{0}}{2 E I}(L – 2 x) \\ \delta_C = \delta_{max} = \frac{M_{0}L^2}{8 E I} \quad \theta_A = \theta_B = \frac{M_o L}{2EI} |
 |
\displaystyle{v=-\frac{q_0 x}{360LE I}(7L^{4} – 10L^2 x^2 + 3Lx^{4} )} \\ \displaystyle{v^\prime=-\frac{q_0 }{360LE I}(7L^{4} – 30L^2 x^2 + 15x^{4} )} \\ \delta_C = {\frac{5q_0 L^{4}}{768E I}}\quad \theta_A = \frac{7q_0 L^{3}}{360E I} \quad \theta_B = \frac{q_0 L^{3}}{45E I} \\ x_1 = 0.5193 L \quad \delta_{max} = 0.00652\frac{q_0L^4}{EI} |
 |
\displaystyle{v=-\frac{q_0 x}{960LE I}(5L^2 – 4x^2)^2} \quad\quad \left( 0 \leq x \leq \frac{L}{2}\right) \\ \displaystyle{v^\prime=-\frac{q_0}{192LE I}(5L^2 – 4x^2)(L^2 – 4x^2)} \quad\quad \left( 0 \leq x \leq \frac{L}{2}\right) \\ \delta_C = \delta_{max} = {\frac{q_0 L^{4}}{120E I}} \quad \theta_A = \theta_B = \frac{5q_0 L^{3}}{192E I} |
 |
\displaystyle{v=-\frac{q_0 L^4}{\pi ^4E I}\sin {\frac{\pi x}{L}}} \quad \displaystyle{v^\prime=-\frac{q_0 L^3}{\pi ^3E I}\cos {\frac{\pi x}{L}}} \\ \delta_C = \delta_{max} = {\frac{q_0 L^{4}}{\pi^4E I}} \quad \theta_A = \theta_B = \frac{q_0 L^{3}}{\pi^3E I} |
| Table H-1 | |
| Deflections and Slopes of Cantilever Beams | |
 |
Notation: v = deflection in the y direction (positive upward) v’ = dv/dx = slope of the deflection curve δ_B = -v(L) = deflection at end B of the beam (positive downward) θ_B = -v^\prime(L) = angle of rotation at end B of the beam (positive clockwise) EI = constant |
 |
\nu=-{\frac{q x^{2}}{24E I}}(6L^{2}-4L x+x^{2})\quad\quad v^\prime= {\frac{q x}{6E I}}(3L^{2} – 3 L x+x^{2}) \\ δ_B = {\frac{q L^4}{8E I}} \quad \theta_B = {\frac{q L^3}{6E I}} |
 |
\displaystyle{v=-\frac{q x^{2}}{24E I}(6a^{2}-4 a x+x^{2})}\qquad\qquad(0\leq x\leq a) \\ \displaystyle{v^\prime=-\frac{q x}{6E I}(3a^{2}- 3 a x+x^{2})}\qquad\qquad(0\leq x\leq a) \\ \displaystyle{v=-\frac{q a^{3}}{24E I}(4x – a)} \quad\quad \displaystyle{v^\prime=-\frac{q a^{3}}{6E I}}\qquad(a\leq x\leq L) \\ At \, x= a : v = -\frac{q a^{4}}{8E I} \quad v^\prime = -\frac{q a^{3}}{6E I}\\ \delta_B = {\frac{q a^{3}}{24E I}(4L – a)}\quad \theta_B = \frac{q a^{3}}{6E I} |
 |
\displaystyle{v=-\frac{qb x^{2}}{12E I}(6L+3 a – 2x)}\qquad\qquad(0\leq x\leq a) \\ \displaystyle{v^\prime= -\frac{qb x}{2E I}(L+ a – x)}\qquad\qquad(0\leq x\leq a) \\ \displaystyle{v=-\frac{q }{24E I}(x^4 -4Lx^3 +6L^2x^2 – 4a^3x + a^4)} \qquad\qquad(a\leq x\leq L) \\ \displaystyle{v^\prime=-\frac{q }{6E I}(x^3 -3Lx^2 + 3L^2x – a^3)} \qquad\qquad(a\leq x\leq L)\\ AT x = a: \, v = -\frac{qa^2b}{12EI}(3L + a) \quad v^\prime = -\frac{qabL}{2EI}\\ \delta_B = {\frac{q }{24E I}(3L^4 -4 a^3L + a^4)}\quad \theta_B = \frac{q }{6E I}(L^3 – a^3) |
 |
v = -\frac{Px^2}{6EI}(3L – x) \quad v^\prime = -\frac{Px}{2EI}(2L – x)\\ \delta_B = {\frac{PL^3}{3E I}}\quad \theta_B = \frac{PL^2}{2E I} |
 |
\displaystyle{v=-\frac{Px^{2}}{6E I}(3a – x)}\quad \displaystyle{v^\prime=-\frac{Px}{2E I}(2a- x)}\qquad\qquad(0\leq x\leq a) \\ \displaystyle{v=-\frac{Pa^{2}}{6E I}(3x – a)} \quad\quad \displaystyle{v^\prime=-\frac{Pa^{2}}{2E I}}\qquad(a\leq x\leq L) \\ At \, x= a : v = -\frac{Pa^{3}}{3E I} \quad v^\prime = -\frac{Pa^{2}}{2E I}\\ \delta_B = {\frac{P a^{2}}{6E I}(3L – a)}\quad \theta_B = \frac{P a^{2}}{2E I} |
 |
\nu=-\frac{M_{0}x^{2}}{2E I}\quad\quad \nu^{\prime}=-\frac{M_{0}x}{E I} \\ \delta_B=-\frac{M_{0}L^{2}}{2E I}\quad\quad \theta_{B}=-\frac{M_{0}L}{E I} |
 |
\displaystyle{v=-\frac{M_0 x^{2}}{2E I}}\qquad \displaystyle{v^\prime=-\frac{M_0 x}{E I}}\qquad(0\leq x\leq a) \\ \displaystyle{v=-\frac{M_0 a}{2E I}}(2x – a) \quad \displaystyle{v^\prime=-\frac{M_0 a}{E I}}\qquad(0\leq x\leq a) \\ At \, x= a : \displaystyle{v=-\frac{M_0 a^{2}}{2E I}}\qquad \displaystyle{v^\prime=-\frac{M_0 a}{E I}}\\ \delta_B = {\frac{M_0 a}{2E I}(2L – a)}\quad \theta_B = \frac{M_0 a}{E I} |
 |
\displaystyle{v=-\frac{q_0 x^{2}}{120LE I}(10L^{3} – 10L^2 x + 5Lx^{2} – x^3)} \\ \displaystyle{v^\prime=-\frac{q_0 x}{24LE I}(4L^{3}- 6L^2 x + 4Lx^{2} – x^3)} \\ \delta_B = {\frac{q_0 L^{4}}{30E I}}\quad \theta_B = \frac{q_0 L^{3}}{24E I} |
 |
\displaystyle{v=-\frac{q_0 x^{2}}{120LE I}(20L^{3} – 10L^2 x + x^3)} \\ \displaystyle{v^\prime=-\frac{q_0 x}{24LE I}(8L^{3}- 6L^2 x + x^3)} \\ \delta_B = {\frac{11q_0 L^{4}}{120E I}}\quad \theta_B = \frac{q_0 L^{3}}{8E I} |
 |
\displaystyle{v=-\frac{q_0 L}{3\pi ^4E I}(48L^{3}\cos {\frac{\pi x}{2L}} – 48L^3 + 3\pi ^3Lx^2 – \pi^3x^3)} \\ \displaystyle{v^\prime=-\frac{q_0 L}{\pi ^3E I}( 2\pi ^2Lx – \pi^2x^2 – 8L^{2}\sin {\frac{\pi x}{2L}})} \\ \delta_B = {\frac{2q_0 L^{4}}{3\pi^4E I}}(\pi^3 – 24)\quad \theta_B = \frac{q_0 L^{3}}{\pi^3E I}(\pi^2 – 8) |