Question 9.5: Determining Critical Speed of a Hollow Shaft A shaft with in......
Determining Critical Speed of a Hollow Shaft
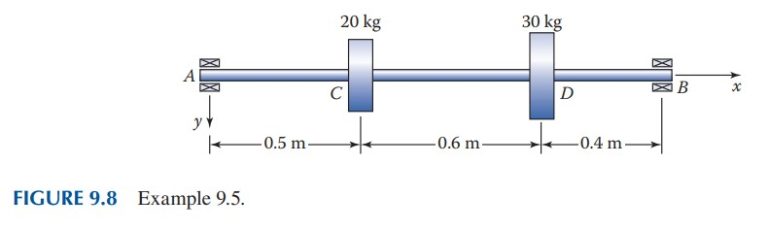
A shaft with inner and outer diameters of d and D , respectively, is mounted between bearings and supporting two wheels, as shown in Figure 9.8. Calculate the critical speed in rpm, applying (a) the Rayleigh method, and (b) the Dunkerley method.
Given: d =30 mm, D =50 mm.
Assumptions: The shaft is made of L =1.5 m long steel having E =210 GPa. The weight of the shaft is ignored. Bearings act as simple supports.
Learn more on how do we answer questions.
The moment of inertia of the cross-section is I=\frac{\pi}{4}\left(25^4-15^4\right)=267 \times 10^3 mm ^4 . The concentrated forces are W_C=20 \times 9.81=196.2 N \text { and } W_D=30 \times 9.81=294.3 N . Static deflections at C and D can be obtained by the equations for Case 6 of Table A.8:
\begin{aligned} & \text { For } a>b: \\ & -\frac{P b\left(L^2-b^2\right)^{3 / 2}}{9 \sqrt{3} E I L} \quad \theta_A=-\frac{P b\left(L^2-b^2\right)}{6 E I L} \quad \upsilon =\frac{P b x}{6 E I L}\left(x^2-L^2+b^2\right) \quad(x \leq a) \\ & x_m=\sqrt{\frac{L^2-b^2}{3}} \quad \theta_B=-\frac{P a\left(L^2-a^2\right)}{6 E I L} \quad \upsilon =\frac{P b(a-x)}{6 E I L}\left(x^2+a^2-2 L x\right) \quad(a \leq x \leq L) \end{aligned} (equations for Case 6 of Table A.8)
\delta=\frac{W b x}{6 L E I}\left[L^2-b^2-x^2\right] \quad(0 \leq x \leq a) (a)
\delta=\frac{W a(L-x)}{6 L E I}\left[2 L x-a^2-x^2\right] \quad(a \leq x \leq L) (b)
Deflection at C . Due to the load at C,[L=1.5 m , b=1 m \text {, and } x=0.5 m \text {, } Equation (a)],
\delta_C^{\prime}=\frac{196.2(1)(0.5)\left(1.5^2-1^2-0.5^2\right)}{6(1.5)\left(267 \times 10^{-9}\right)\left(210 \times 10^9\right)}=0.194 mm (b)
Owing to the load a D [L=1.5 m , b=0.4 m \text {, and } x=0.5 m \text {, Equation (a) }] \text {, }
\delta_C^{\prime \prime}=\frac{294.3(0.4)(0.5)\left(1.5^2-0.4^2-0.5^2\right)}{6(1.5)(267 \times 210)}=0.215 mm
The total deflection is then
\delta_C=0.194+0.215=0.409 mm
Deflection at D . Due to the load at C,[a=0.5 m , x=1.1 m , \text { Equation (b) }] \text {, }
\delta_D^{\prime}=\frac{196.2(0.5)(15-1.1)\left[2(1.5)(1.1)-0.5^2-1.1^2\right]}{6(1.5)(267 \times 210)}=0.143 mm
Owing to the load at D [b=0.4 m , x=1.1 m \text {, Equation (a) }] \text {, }
\delta_D^{\prime \prime}=\frac{294.3(0.4)(1.1)\left(1.5^2-0.4^2-1.1^2\right)}{6(1.5)(267 \times 210)}=0.226 mm
and hence,
\delta_D=0.143+0.226=0.369 mm
a. Using Equation (9.18) with m =2, we have
n_{c r}=\frac{1}{2 \pi}\left[\frac{g\left(W_1 \delta_1+W_2 \delta_2+\cdots+W_m \delta_m\right)}{W_1 \delta_1^2+W_2 \delta_2^2+\cdots+W_m \delta_m^2}\right]^{1 / 2}=\frac{1}{2 \pi} \sqrt{\frac{g \Sigma W \delta}{\Sigma W \delta^2}} (9.18)
\begin{aligned} n_{c r} & =\frac{1}{2 \pi}\left[\frac{9.81\left(196.2 \times 0.409 \times 10^{-3}+294.3 \times 0.369 \times 10^{-3}\right)}{196.2\left(0.409 \times 10^{-3}\right)^2+294.3\left(0.369 \times 10^{-3}\right)^2}\right]^{1 / 2} \\ & =25.37 cps =1522 rpm \end{aligned}
b. Equation (9.19) may be rewritten as
\frac{1}{n_{c r}^2}=\frac{1}{n_1^2}+\frac{1}{n_2^2}+\cdots+\frac{1}{n_m^2} (9.19)
\frac{1}{n_{c r}^2}=\frac{1}{n_{c r, C}^2}+\frac{1}{n_{c r, D}^2} (c)
Solving,
n_{c r}=\frac{n_{c r, C} \cdot n_{c r, D}}{\sqrt{n_{c r, C}^2+n_{c r, D}^2}} (9.21)
where
n_{c r, C}=\frac{1}{2 \pi} \sqrt{\frac{g}{\delta_C^{\prime}}}=\frac{1}{2 \pi} \sqrt{\frac{9.81}{0.194\left(10^{-3}\right)}}=35.79 cps =2147 rpm
n_{c r, D}=\frac{1}{2 \pi} \sqrt{\frac{g}{\delta_D^{\prime \prime}}}=\frac{1}{2 \pi} \sqrt{\frac{9.81}{0.226\left(10^{-3}\right)}}=33.16 cps =1990 rpm
Equation (9.21) is therefore
n_{c r}=\frac{(2147)(1990)}{\sqrt{(2147)^2+(1990)^2}}=1459 rpm
Comments: A comparison of the results obtained shows that the Rayleigh’s equation overestimates and the Dunkerley’s equation underestimates the critical speed. It follows that the actual critical speed is between 1459 and 1522 rpm. The design of the shaft should avoid this operation range.
| TABLE A.8 Deflections and Slopes of Variously Loaded Beams |
|||
| Load and Support | Maximum Deflection | Slope at End | Equation of Elastic Curve |
\quad\quad\quad\quad\quad\quad\quad\quad |
-\frac{P L^3}{3 E I} | -\frac{P L^2}{3 E I} | \upsilon =\frac{P x^2}{3 E I}(x-3 L) |
\quad\quad\quad\quad\quad\quad\quad\quad\quad |
-\frac{M L^2}{2 E I} | -\frac{M L}{E I} | \upsilon =\frac{M x^2}{2 E I} |
\quad\quad\quad\quad\quad\quad\quad\quad\quad |
-\frac{w L^4}{8 E I} | -\frac{w L^3}{6 E I} | \upsilon =\frac{w x^2}{24 E I}\left(x^2-4 L x+6 L^2\right) |
\quad\quad\quad\quad\quad\quad\quad\quad\quad |
-\frac{w_0 L^4}{30 E I} | -\frac{w_0 L^3}{24 E I} | \upsilon =\frac{w x^2}{120 E I}\left(x^2-4 L x+6 L^3\right) |
\quad\quad\quad\quad\quad\quad\quad\quad\quad |
-\frac{P L^3}{48 E I} | \pm \frac{P L^2}{16 E I} | \upsilon =\frac{P x}{48 E I}\left(4 x^2-3 L^2\right) \quad(x \leq L / 2) |
\quad\quad\quad\quad\quad\quad\quad\quad |
For a>b : \\ \begin{gathered} -\frac{P b\left(L^2-b^2\right)^{3 / 2}}{9 \sqrt{3} E I L} \\ x_m=\sqrt{\frac{L^2-b^2}{3}} \end{gathered} | \begin{aligned} & \theta_A=-\frac{P b\left(L^2-b^2\right)}{6 E I L} \\ & \theta_B=-\frac{P a\left(L^2-a^2\right)}{6 E I L} \end{aligned} | \begin{aligned} & \upsilon =\frac{P b x}{6 E I L}\left(x^2-L^2+b^2\right) \quad(x \leq a) \\ & \upsilon =\frac{P b(a-x)}{6 E I L}\left(x^2+a^2-2 L x\right) \quad(a \leq x \leq L) \end{aligned} |
\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad |
\pm \frac{M L^3}{9 \sqrt{3} E I} | \begin{gathered} \theta_A=-\frac{M L}{6 E I} \\ \theta_B=-\frac{M L}{3 E I} \end{gathered} | \upsilon =\frac{M x}{6 E I L}\left(x^2-L^2\right) |
\quad\quad\quad\quad\quad\quad\quad\quad\quad |
-\frac{5 w L^4}{384 E I} | \pm \frac{w L^3}{24 E I} | \upsilon =\frac{w x}{24 E I}\left(x^3-2 L x^2+L^3\right) |
\quad\quad\quad\quad\quad\quad\quad\quad\quad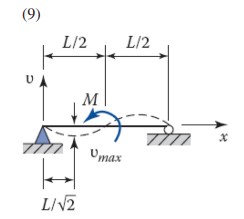 |
\pm \frac{M L^2}{36 \sqrt{12} E I} | \pm \frac{M L}{24 E I} | \upsilon =\frac{M x}{24 E I L}\left(4 x^2-L^2\right) \quad(x \geq L / 2) |
\quad\quad\quad\quad\quad\quad\quad\quad\quad |
-\frac{P b^2 L}{3 E I} | \begin{aligned} & \theta_A=-\frac{P a b}{6 E I} \\ & \theta_B=-\frac{P b}{6 E I}(2 L+b) \end{aligned} | \upsilon =\frac{P b x}{6 a E I}\left(a^2-x^2\right) \quad(0 \leq x \leq a) |