Question 10.5: A fixed-end beam AB supports a uniform load of intensity q a......
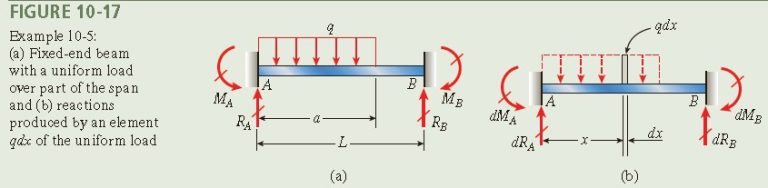
A fixed-end beam AB supports a uniform load of intensity q acting over part of the span (Fig. 10-17a).
Determine the reactions of this beam (that is, find the fixed-end moments and fixed-end forces).
Learn more on how do we answer questions.
Use a four-step problem-solving approach.
1. Conceptualize: Find the reactions of this beam by using the principle of superposition together with the results obtained in Example 10-4. In that example, reactions were found for a fixed-end beam subjected to a concentrated load P acting at distance a from the left-hand end [see Fig. 10-15a and Eqs. (10-30) and (10-31)].
In order to apply those results to the uniform load of Fig. 10-17a, treat an element of the uniform load as a concentrated load of magnitude qdx acting at distance x from the left-hand end (Fig. 10-17b). Then, using the formulas derived in Example 10-4, find the reactions caused by this element of load.
Finally, by integrating over the length a of the uniform load, obtain the reactions due to the entire uniform load.
2. Categorize:
Fixed-end moments: Begin with the moment reactions using Eqs. (10-30a and b) of Example 10-4. To obtain the moments caused by the element qdx of the uniform load (compare Fig. 10-17b with Fig. 10-15a), replace P with qdx, a with x, and b with L – x. Thus, the fixed-end moments due to the element of load (Fig. 10-17b) are
\quad\quad\quad\quad d M_{A}=\frac{q x(L-x)^{2}d x}{L^{2}}\;\;\;\;d M_{B}=\frac{q x^{2}(L-x)d x}{L^{2}}
3. Analyze: Integrate over the loaded part of the beam to get the fixed-end moments due to the entire uniform load:
\quad\quad\quad\quad M_{A}=\int\!d M_{A}=\frac{q}{L^{2}}~\int_{0}^{a}\!x(L-x)^{2}d x=\frac{q a^{2}}{12L^{2}}(6L-8a L+\,3a^{2})\quad\quad (10-35a) \\ \quad\quad\quad\quad M_{B}\,=\,\int d M_{B}=\frac{q}{L^{2}}\!\int_{0}^{a}\!x^{2}(L\,-\,x)d x=\frac{q a^{3}}{12L^{2}}(4L\,-\,3{{{a}}}) \quad\quad (10-35b)
Fixed-end forces: Proceed in a similar manner as for the fixed-end moments, but use Eqs. (10-31a and b) to obtain the following expressions for the fixedend forces due to the element qdx of load:
\quad\quad\quad\quad M_{A}\,=\,{\frac{{{P}}a b^{2}}{L^{2}}}\quad M_{B}\,=\,{\frac{{{P}}a^{2}b}{L^{2}}}\quad\quad(10-30a,b)
\quad\quad\quad\quad R_{A}=\frac{P b^{2}}{L^{3}{}}\;(L+2a)\qquad R_{B}=\frac{P a^{2}}{L^{3}}\;(L+2b)\quad\quad(10-31a,b)
\quad\quad\quad\quad d R_{_A}={\frac{q(L-x)^{2}(L+2x)d x}{L^{3}}}\ \ \ \ \ d R_{B}={\frac{q x^{2}(3L-2x)d x}{L^{3}}}
Integration gives
\quad\quad\quad\quad R_{A}=\int d R_{A}=\frac{q}{L^{3}}\!\!\int_{0}^{a}(L-x)^{2}(L+2x)d x=\frac{q a}{2L^{3}}(2L^{3}-2L a^{2}+a^{3})\quad\quad (10-36a) \\ \quad\quad\quad\quad R_{B}\,=\,\int{d R_{B}}=\frac{q}{L^{3}}\,\int_{0}^{a}\!x^{2}\,(3L-2x)\,d x=\frac{q a^{3}}{2L^{3}}(2L-a) \quad\quad(10-36b)
Thus, all reactions (fixed-end moments and fixed-end forces) have been found.
4. Finalize:
Uniform load acting over the entire length of the beam: When the load acts over the entire span (Fig. 10-18), obtain the reactions by substituting a = L into the preceding equations, yielding
\quad\quad\quad\quad M_{A}=M_{B}={\frac{q L^{2}}{12}}\quad R_{A}=R_{B}={\frac{q L}{2}}\quad\quad(10-37a,b)
The deflection at the midpoint of a uniformly loaded beam is also of interest. The simplest way to obtain this deflection is to use the method of superposition. The first step is to remove the moment restraints at the supports and obtain a released structure in the form of a simple beam. The downward deflection at the midpoint of a simple beam due to a uniform load (from Case 1, Table H-2) is
\quad\quad\quad\quad (\delta_{C})_{1}={\frac{5q L^{4}}{384E I}}\quad\quad(a)
and the upward deflection at the midpoint due to the end moments (from Case 10, Table H-2) is
\quad\quad\quad\quad (\delta_{C})_{2}={\frac{M_{A}L^{2}}{8E I}}={\frac{(q L^{2}/12)L^{2}}{8E I}}={\frac{q L^{4}}{96E I}}\quad\quad(b)
Thus, the final downward deflection of the original fixed-end beam (Fig. 10-18) is
\quad\quad\quad\quad \delta_{C}=(\delta_{C})_{1}-(\delta_{ C})_{2}
Substitute for the deflections from Eqs. (a) and (b) to get
\quad\quad\quad\quad \delta_{C}={\frac{q{{L}}^{4}}{384E I}}\quad\quad(10-38)
This deflection is one-fifth of the deflection at the midpoint of a simple beam with a uniform load [Eq. (a)], again illustrating the stiffening effect of fixity at the ends of the beam.
| Table H-2 | |
| Deflections and Slopes of Simple Beams | |
 |
Notation: v = deflection in the y direction (positive upward) v’ = dv/dx = slope of the deflection curve δ_C = -v(L/2) = deflection at end B of the beam (positive downward) x_1 = distance from support A to point of maximum deflection \delta_{max} = -v_{max} = maximum deflection (positive downward) \theta_A = -v^\prime(0) = angle of rotation at left-hand end of the beam (positive clockwise) \theta_B = v^\prime(L) = angle of rotation at right-hand end of the beam (positive counterclockwise) EI = constant |
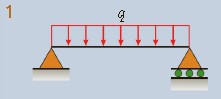 |
\begin{array}{l}{{\nu=-{\frac{q x}{24E I}}(L^{3}-2L x^{2}+x^{3})}}\\ {{\nu^\prime=-{\frac{q}{24E I}}(L^{3}-6L x^{2}+4x^{3})}}\\ {{\mathrm{~\delta_{C}= \delta_{max}= -\frac{5qL^4}{384E I} \quad \theta_A = \theta_B = \frac{qL^3}{24EI}}}}\end{array} |
 |
\begin{array}{l}{{\nu=-{\frac{q x}{384E I}}(9L^{3} – 24L x^{2} + 16x^{3})}} \quad\quad \left(0\leq x\leq{\frac{L}{2}}\right) \\ {{\nu^\prime=-{\frac{q}{384E I}}(9L^{3} – 72L x^{2} + 64x^{3})}}\quad\quad \left(0\leq x\leq{\frac{L}{2}}\right) \\ \nu=-{\frac{q L}{384E I}}(8x^{3} – 24L x^{2} + 17L^{2}x – L^3) \quad\quad \left(\frac{L}{2}\leq x\leq {L}\right) \\ \nu^\prime=-{\frac{q L}{384E I}}(24x^{2} – 48L x + 17L^{2}) \quad\quad \left(\frac{L}{2}\leq x\leq {L}\right) \\ {{\mathrm{~\delta_{C}= -\frac{5qL^4}{768E I} \, \theta_A = \frac{3qL^3}{128EI} \, \theta_B = \frac{7qL^3}{384EI}}}} \end{array} |
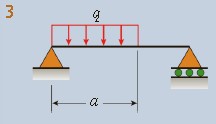 |
\begin{array}{l}{{\nu=-{\frac{q x}{24LE I}}(a^{4} – 4a^3L +4a^2L^2 + 2a^2x^2 – 4aLx^2 + Lx^{3})}} \quad\quad (0 \leq x \leq a)\\ {{\nu^\prime=-{\frac{q}{24LE I}}(a^{4} – 4a^3L +6a^2L^2 + 6a^2x^2 – 12aLx^2 – 4Lx^{3})}} \quad\quad (0 \leq x \leq a) \\ \nu=-{\frac{q a^2}{24LE I}}(-a^{2}L + 4L^{2}x + a^2 x -6 Lx^2 + 2x^3) \quad\quad (a \leq x \leq {L})\\ \nu^\prime=-{\frac{q A^2}{24LE I}}(4L^{2} + a^2 – 12Lx + 6x^2) \quad\quad\quad\quad (a \leq x \leq {L}) \\ {{\mathrm{~ \theta_A = \frac{qa^2}{24LEI}(2L – a)^2 \, \theta_B = \frac{qa^2}{24LEI}(2L^2 – a^2)}}} \end{array} |
 |
v=-{\frac{P x}{48E I}}(3L^{2}-4x^{2})\;\;\;\;\;v^{\prime}=-{\frac{P}{16E I}}(L^{2}-4x^{2})\;\;\;\;\left(0\leq x\leq{\frac{L}{2}}\right) \\ \delta_C = \delta_{max} = {\frac{PL^3}{48E I}}\quad\quad \theta_A = \theta_B = {\frac{PL^2}{16E I}} |
 |
\nu=-{\frac{P b x}{6L E I}}(L^{2}\,-\,b^{2}\,-\,x^{2}\,)\quad\nu^{\prime}=-{\frac{P b}{6L E I}}(L^{2}\,-\,b^{2}\,-\,3x^{2}\,)\quad(0\leq\,x\leq a) \\ \theta_A = \frac{Pab(L + a)}{6LEI} \quad \theta_B = \frac{Pab(L + a)}{6LEI} \\ If \, a ≥ b,\quad \delta_C = \frac{Pb(3L^2 – 4b^2)}{48EI} \quad If \, a \leq b,\quad \delta_C = \frac{Pa(3L^2 – 4a^2)}{48EI} \\ If \, a ≥ b,\quad x_1 = \sqrt{\frac{L^2 – b^2}{3}} \quad\quad and \quad \delta_{max}= \frac{Pb(L^2 – b^2)^{3/2}}{9\sqrt{3}LEI} |
 |
v=-{\frac{P x}{6E I}}(3aL – 3a^{2} – x^2)\;\;\;\;\;v^{\prime}=-{\frac{P}{2E I}}(aL – a^{2} – x^{2})\;\;\;\;\left(0\leq x\leq a\right) \\ v=-{\frac{P a}{6E I}}(3Lx – 3x^{2} – a^2)\;\;\;\;\;v^{\prime}=-{\frac{Pa}{2E I}}(L – 2 x)\;\;\;\;\left(a\leq x\leq L – a\right) \\ \delta_C = \delta_{max} = {\frac{Pa}{24E I}}(3L^2 – 4a^2)\quad\quad \theta_A = \theta_B = {\frac{P a (L- a)}{2E I}} |
 |
\nu=-\frac{M_{0}x}{6 LE I}(2L^{2} – 3L x + x^{2}) \quad {\nu}^{\prime}=-\frac{M_{0}}{6L E I}(2L^{2}-6L x+3x^{2}) \\ \delta_C = \frac{M_{0}L^2}{16 E I} \quad \theta_A = \frac{M_0L}{3EI} \quad \theta_B = \frac{M_0 L}{6EI} \\ x_1 = L {{\Bigg\lgroup}}1 – \frac{\sqrt{3}}{3} {{\Bigg\rgroup}} \quad and \quad \delta_{max} = \frac{M_0 L^2}{9\sqrt{3}EI} |
 |
\nu=-\frac{M_{0}x}{24 LE I}(L^{2} – 4x^{2}) \quad {\nu}^{\prime}=-\frac{M_{0}}{24L E I}(L^{2}-12x^{2}) \quad \left(0 \leq x \leq \frac{L}{2} \right) \\ \delta_C = 0 \quad \theta_A = \frac{M_0L}{24EI} \quad \theta_B = \frac{M_0 L}{24EI} |
 |
\displaystyle{v=-\frac{M_0 x}{6LE I}}(6aL – 3a^2 – 2 L^2 – x^2)\qquad(0\leq x\leq a) \\ \displaystyle{v^\prime=-\frac{M_0 }{6LE I}}(6aL – 3a^2 – 2 L^2 – 3x^2)\qquad(0\leq x\leq a) \\ At \, x= a : \displaystyle{v=-\frac{M_0 ab}{3LE I}}(2a – L)\qquad \displaystyle{v^\prime=-\frac{M_0 }{3LE I}}(3aL – 3a^2 – L^2)\\ \theta_A = {\frac{M_0 }{6LE I}(6 a L – 3a^2 – 2L^2)}\quad \theta_B = \frac{M_0 }{6LE I}(3a^2 – L^2) |
 |
\nu=-\frac{M_{0}x}{2E I}(L – x ) \quad {\nu}^{\prime}=-\frac{M_{0}}{2 E I}(L – 2 x) \\ \delta_C = \delta_{max} = \frac{M_{0}L^2}{8 E I} \quad \theta_A = \theta_B = \frac{M_0 L}{2EI} |
 |
\displaystyle{v=-\frac{q_0 x}{360LE I}(7L^{4} – 10L^2 x^2 + 3Lx^{4} )} \\ \displaystyle{v^\prime=-\frac{q_0 }{360LE I}(7L^{4} – 30L^2 x^2 + 15x^{4} )} \\ \delta_C = {\frac{5q_0 L^{4}}{768E I}}\quad \theta_A = \frac{7q_0 L^{3}}{360E I} \quad \theta_B = \frac{q_0 L^{3}}{45E I} \\ x_1 = 0.5193 L \quad \delta_{max} = 0.00652\frac{q_0L^4}{EI} |
 |
\displaystyle{v=-\frac{q_0 x}{960LE I}(5L^2 – 4x^2)^2} \quad\quad \left( 0 \leq x \leq \frac{L}{2}\right) \\ \displaystyle{v^\prime=-\frac{q_0}{192LE I}(5L^2 – 4x^2)(L^2 – 4x^2)} \quad\quad \left( 0 \leq x \leq \frac{L}{2}\right) \\ \delta_C = \delta_{max} = {\frac{q_0 L^{4}}{120E I}} \quad \theta_A = \theta_B = \frac{5q_0 L^{3}}{192E I} |
 |
\displaystyle{v=-\frac{q_0 L^4}{\pi ^4E I}\sin {\frac{\pi x}{L}}} \quad \displaystyle{v^\prime=-\frac{q_0 L^3}{\pi ^3E I}\cos {\frac{\pi x}{L}}} \\ \delta_C = \delta_{max} = {\frac{q_0 L^{4}}{\pi^4E I}} \quad \theta_A = \theta_B = \frac{q_0 L^{3}}{\pi^3E I} |

