Question 10.3: A two-span continuous beam ABC supports a uniform load of in......
A two-span continuous beam ABC supports a uniform load of intensity q, as shown in Fig. 10-14a. Each span of the beam has a length L. Using the method of superposition, determine all reactions for this beam.

Learn more on how do we answer questions.
Use a four-step problem-solving approach.
1. Conceptualize: This beam has three unknown reactions (R_A, R_B, ~ and ~ R_C). Since there are two equations of equilibrium for the beam as a whole, it is statically
indeterminate to the first degree. For convenience, select the reaction R_B at the middle support as the redundant.
2. Categorize:
Equations of equilibrium: Express the reactions R_A ~ and ~ R_C in terms of the redundant R_B by means of two equations of equilibrium. The first equation, which is for equilibrium of moments about point B, shows that R_A ~ and ~ R_C are equal. The second equation, which is for equilibrium in the vertical direction, yields
\quad\quad\quad\quad R_{A}=R_{C}=q L-{\frac{R_{B}}{2}}\quad\quad(a)
Equation of compatibility: Because the reaction R_B is selected as the redundant, the released structure is a simple beam with supports at A and C (Fig. 10-14b).
The deflections at point B in the released structure due to the uniform load q and the redundant R_B are shown in Figs. 10-14c and d, respectively. Note that the deflections are denoted (\delta_B)_1 ~ and ~ (\delta_B)_2. The superposition of these deflections must produce the deflection \delta_B in the original beam at point B. Since the latter deflection is equal to zero, the equation of compatibility is
\quad\quad\quad\quad \delta_{B}=(\delta_{B})_{1}-(\delta_{B})_{2}=0\quad\quad(b)
in which the deflection (\delta_B)_1 is positive downward, and the deflection (\delta_B)_2 is positive upward.
Force-displacement relations: The deflection (\delta_B)_1 caused by the uniform load acting on the released structure (Fig. 10-14c) is obtained from Table H-2, Case 1 as
\quad\quad\quad\quad (\delta_{B})_{1}=\frac{5 q(2{L})^{4}}{384E I}=\frac{5 q{L}^{4}}{24{L}}
where 2L is the length of the released structure. The deflection (\delta_B)_2 produced by the redundant (Fig. 10-14d) is
\quad\quad\quad\quad (\delta_{B})_{2}=\frac{{R}_{B}(2{L})^{3}}{48E{I}}=\frac{{R}_{B}{L}^3}{6E{I}}
as obtained from Table H-2, Case 4.
3. Analyze:
Reactions: The equation of compatibility pertaining to the vertical deflection at point B [Eq. (b)] now becomes
\quad\quad\quad\quad \delta_{B}=\frac{5 q L^{4}}{24E I}-\frac{R_{B}L^{3}}{6E I}=0\quad\quad(c)
from which the reaction at the middle support is
\quad\quad\quad\quad R_{B}={\frac{5q L}{4}}\quad\quad(10-28)
The other reactions are obtained from Eq. (a):
\quad\quad\quad\quad R_{A}=R_{C}={\frac{3q L}{8}}\quad\quad(10-29)
With the reactions known, the shear forces, bending moments, stresses, and deflections can be found without difficulty.
4. Finalize: The purpose of this example is to demonstrate the method of superposition, so all steps were described in the analysis. However, this particular beam (Fig. 10-14a) can be analyzed by inspection because of the symmetry of the beam and its loading.
From symmetry, the slope of the beam at the middle support must be zero; therefore, each half of the beam is in the same condition as a propped cantilever beam with a uniform load (see, for instance, Fig. 10-6). Consequently, all of the previous results for a propped cantilever beam with a uniform load [Eqs. (10-1) to (10-12)] can be adapted immediately to the continuous beam of Fig. 10-14a.
| Table H-2 | |
| Deflections and Slopes of Simple Beams | |
 |
Notation: v = deflection in the y direction (positive upward) v’ = dv/dx = slope of the deflection curve δ_C = -v(L/2) = deflection at end B of the beam (positive downward) x_1 = distance from support A to point of maximum deflection \delta_{max} = -v_{max} = maximum deflection (positive downward) \theta_A = -v^\prime(0) = angle of rotation at left-hand end of the beam (positive clockwise) \theta_B = v^\prime(L) = angle of rotation at right-hand end of the beam (positive counterclockwise) EI = constant |
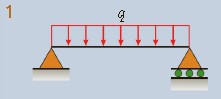 |
\begin{array}{l}{{\nu=-{\frac{q x}{24E I}}(L^{3}-2L x^{2}+x^{3})}}\\ {{\nu^\prime=-{\frac{q}{24E I}}(L^{3}-6L x^{2}+4x^{3})}}\\ {{\mathrm{~\delta_{C}= \delta_{max}= -\frac{5qL^4}{384E I} \quad \theta_A = \theta_B = \frac{qL^3}{24EI}}}}\end{array} |
 |
\begin{array}{l}{{\nu=-{\frac{q x}{384E I}}(9L^{3} – 24L x^{2} + 16x^{3})}} \quad\quad \left(0\leq x\leq{\frac{L}{2}}\right) \\ {{\nu^\prime=-{\frac{q}{384E I}}(9L^{3} – 72L x^{2} + 64x^{3})}}\quad\quad \left(0\leq x\leq{\frac{L}{2}}\right) \\ \nu=-{\frac{q L}{384E I}}(8x^{3} – 24L x^{2} + 17L^{2}x – L^3) \quad\quad \left(\frac{L}{2}\leq x\leq {L}\right) \\ \nu^\prime=-{\frac{q L}{384E I}}(24x^{2} – 48L x + 17L^{2}) \quad\quad \left(\frac{L}{2}\leq x\leq {L}\right) \\ {{\mathrm{~\delta_{C}= -\frac{5qL^4}{768E I} \, \theta_A = \frac{3qL^3}{128EI} \, \theta_B = \frac{7qL^3}{384EI}}}} \end{array} |
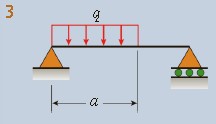 |
\begin{array}{l}{{\nu=-{\frac{q x}{24LE I}}(a^{4} – 4a^3L +4a^2L^2 + 2a^2x^2 – 4aLx^2 + Lx^{3})}} \quad\quad (0 \leq x \leq a)\\ {{\nu^\prime=-{\frac{q}{24LE I}}(a^{4} – 4a^3L +6a^2L^2 + 6a^2x^2 – 12aLx^2 – 4Lx^{3})}} \quad\quad (0 \leq x \leq a) \\ \nu=-{\frac{q a^2}{24LE I}}(-a^{2}L + 4L^{2}x + a^2 x -6 Lx^2 + 2x^3) \quad\quad (a \leq x \leq {L})\\ \nu^\prime=-{\frac{q A^2}{24LE I}}(4L^{2} + a^2 – 12Lx + 6x^2) \quad\quad\quad\quad (a \leq x \leq {L}) \\ {{\mathrm{~ \theta_A = \frac{qa^2}{24LEI}(2L – a)^2 \, \theta_B = \frac{qa^2}{24LEI}(2L^2 – a^2)}}} \end{array} |
 |
v=-{\frac{P x}{48E I}}(3L^{2}-4x^{2})\;\;\;\;\;v^{\prime}=-{\frac{P}{16E I}}(L^{2}-4x^{2})\;\;\;\;\left(0\leq x\leq{\frac{L}{2}}\right) \\ \delta_C = \delta_{max} = {\frac{PL^3}{48E I}}\quad\quad \theta_A = \theta_B = {\frac{PL^2}{16E I}} |
 |
\nu=-{\frac{P b x}{6L E I}}(L^{2}\,-\,b^{2}\,-\,x^{2}\,)\quad\nu^{\prime}=-{\frac{P b}{6L E I}}(L^{2}\,-\,b^{2}\,-\,3x^{2}\,)\quad(0\leq\,x\leq a) \\ \theta_A = \frac{Pab(L + a)}{6LEI} \quad \theta_B = \frac{Pab(L + a)}{6LEI} \\ If \, a ≥ b,\quad \delta_C = \frac{Pb(3L^2 – 4b^2)}{48EI} \quad If \, a \leq b,\quad \delta_C = \frac{Pa(3L^2 – 4a^2)}{48EI} \\ If \, a ≥ b,\quad x_1 = \sqrt{\frac{L^2 – b^2}{3}} \quad\quad and \quad \delta_{max}= \frac{Pb(L^2 – b^2)^{3/2}}{9\sqrt{3}LEI} |
 |
v=-{\frac{P x}{6E I}}(3aL – 3a^{2} – x^2)\;\;\;\;\;v^{\prime}=-{\frac{P}{2E I}}(aL – a^{2} – x^{2})\;\;\;\;\left(0\leq x\leq a\right) \\ v=-{\frac{P a}{6E I}}(3Lx – 3x^{2} – a^2)\;\;\;\;\;v^{\prime}=-{\frac{Pa}{2E I}}(L – 2 x)\;\;\;\;\left(a\leq x\leq L – a\right) \\ \delta_C = \delta_{max} = {\frac{Pa}{24E I}}(3L^2 – 4a^2)\quad\quad \theta_A = \theta_B = {\frac{P a (L- a)}{2E I}} |
 |
\nu=-\frac{M_{0}x}{6 LE I}(2L^{2} – 3L x + x^{2}) \quad {\nu}^{\prime}=-\frac{M_{0}}{6L E I}(2L^{2}-6L x+3x^{2}) \\ \delta_C = \frac{M_{0}L^2}{16 E I} \quad \theta_A = \frac{M_0L}{3EI} \quad \theta_B = \frac{M_0 L}{6EI} \\ x_1 = L {{\Bigg\lgroup}}1 – \frac{\sqrt{3}}{3} {{\Bigg\rgroup}} \quad and \quad \delta_{max} = \frac{M_0 L^2}{9\sqrt{3}EI} |
 |
\nu=-\frac{M_{0}x}{24 LE I}(L^{2} – 4x^{2}) \quad {\nu}^{\prime}=-\frac{M_{0}}{24L E I}(L^{2}-12x^{2}) \quad \left(0 \leq x \leq \frac{L}{2} \right) \\ \delta_C = 0 \quad \theta_A = \frac{M_0L}{24EI} \quad \theta_B = \frac{M_0 L}{24EI} |
 |
\displaystyle{v=-\frac{M_0 x}{6LE I}}(6aL – 3a^2 – 2 L^2 – x^2)\qquad(0\leq x\leq a) \\ \displaystyle{v^\prime=-\frac{M_0 }{6LE I}}(6aL – 3a^2 – 2 L^2 – 3x^2)\qquad(0\leq x\leq a) \\ At \, x= a : \displaystyle{v=-\frac{M_0 ab}{3LE I}}(2a – L)\qquad \displaystyle{v^\prime=-\frac{M_0 }{3LE I}}(3aL – 3a^2 – L^2)\\ \theta_A = {\frac{M_0 }{6LE I}(6 a L – 3a^2 – 2L^2)}\quad \theta_B = \frac{M_0 }{6LE I}(3a^2 – L^2) |
 |
\nu=-\frac{M_{0}x}{2E I}(L – x ) \quad {\nu}^{\prime}=-\frac{M_{0}}{2 E I}(L – 2 x) \\ \delta_C = \delta_{max} = \frac{M_{0}L^2}{8 E I} \quad \theta_A = \theta_B = \frac{M_0 L}{2EI} |
 |
\displaystyle{v=-\frac{q_0 x}{360LE I}(7L^{4} – 10L^2 x^2 + 3Lx^{4} )} \\ \displaystyle{v^\prime=-\frac{q_0 }{360LE I}(7L^{4} – 30L^2 x^2 + 15x^{4} )} \\ \delta_C = {\frac{5q_0 L^{4}}{768E I}}\quad \theta_A = \frac{7q_0 L^{3}}{360E I} \quad \theta_B = \frac{q_0 L^{3}}{45E I} \\ x_1 = 0.5193 L \quad \delta_{max} = 0.00652\frac{q_0L^4}{EI} |
 |
\displaystyle{v=-\frac{q_0 x}{960LE I}(5L^2 – 4x^2)^2} \quad\quad \left( 0 \leq x \leq \frac{L}{2}\right) \\ \displaystyle{v^\prime=-\frac{q_0}{192LE I}(5L^2 – 4x^2)(L^2 – 4x^2)} \quad\quad \left( 0 \leq x \leq \frac{L}{2}\right) \\ \delta_C = \delta_{max} = {\frac{q_0 L^{4}}{120E I}} \quad \theta_A = \theta_B = \frac{5q_0 L^{3}}{192E I} |
 |
\displaystyle{v=-\frac{q_0 L^4}{\pi ^4E I}\sin {\frac{\pi x}{L}}} \quad \displaystyle{v^\prime=-\frac{q_0 L^3}{\pi ^3E I}\cos {\frac{\pi x}{L}}} \\ \delta_C = \delta_{max} = {\frac{q_0 L^{4}}{\pi^4E I}} \quad \theta_A = \theta_B = \frac{q_0 L^{3}}{\pi^3E I} |
